题目内容
下列各图案都是由三个几何图组成：
它们都是按一定的规律排列组合而成的：图案（2）是把图案（1）中的第三个图形移到第一个图形的位置排列而成的，图案（3）是把图案（2）中的第三个图形移到第一个图形的位置排列而成的，…，依照上述图案的排列规律，图案（2011）中的第二个图形是________（填“圆”或“三角形”或“正方形”）
解：观察四个图案发现每三个一循环，
∵2011÷3=670…1，
∴第2011个图案和第1个图案一样，
∴第二个图形是三角形，
故答案为三角形．
分析：首先从四个图案中找到规律，然后利用规律得到答案即可．
点评：本题考查了图形的变化类问题，解题的关键是从中找到图案的规律．
∵2011÷3=670…1，
∴第2011个图案和第1个图案一样，
∴第二个图形是三角形，
故答案为三角形．
分析：首先从四个图案中找到规律，然后利用规律得到答案即可．
点评：本题考查了图形的变化类问题，解题的关键是从中找到图案的规律．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
图1是由若干个小圆圈堆成的一个图案，最上面一层有2个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．完成下列问题：
（1）每一层的圆圈个数与层数的关系为：
| 层数 | 1 | 2 | 3 | … | n |
| 每层圆圈个数 | … |
将图1倒置后与原图1拼成图2的形状，则图2中每层圆圈个数为________；n层圆圈总数为________；由于图2中圆圈个数是图1中的________倍，可以得出图1中所有圆圈的个数为________．
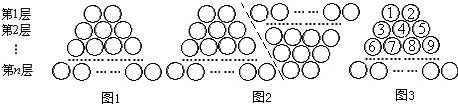
（3）假设图1中的圆圈共有10层，我们自上往下，在每个圆圈中都按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层从左边数第三个圆圈中的数是________．
