题目内容
如图，⊙O是边长为2的等边三角形ABC的内切圆，则图中阴影部分的面积为________．
分析：先求出三角形ABC的面积，从而求出内切圆的半径，进而可求出圆的面积．图中阴影部分的面积=S△ABC-S⊙O．
解答：
解：连接OA，OD（AB上的内切点）．由于等边三角形的内心就是它的外心，可得AD=
AB=1，∠OAB=∠CAB=30°；在Rt△OAD中，tan30°=
，即
=
，得0D=．∴图中阴影部分的面积等于S△ABC-S⊙O=
×22-π（）2=
π．点评：本题考查等边三角形的性质及内切圆的概念和计算．
练习册系列答案
每课必练系列答案
巧学巧练系列答案
相关题目
14、如图，O是边长为6的等边三角形ABC内的任意一点，且OD∥BC，交AB于点D，OF∥AB，交AC于F，OE∥AC，交BC于E．则OD+OE+OF的值（ ）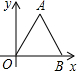
如图，△AOB是边长为5的等边三角形，则A，B两点的坐标分别是A
如图，△ABC是边长为2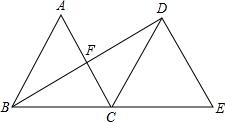
（2012•湘潭）如图，△ABC是边长为3的等边三角形，将△ABC沿直线BC向右平移，使B点与C点重合，得到△DCE，连接BD，交AC于F．
如图，AO是边长为2的等边△ABC的高，点D是AO上的一个动点（点D不与点A、O重合），以CD为一边在AC下方作等边△CDE，连结BE并延长，交AC的延长线于点F．