题目内容
如图两电线杆AB=4米，CD=2米，AB、CD都垂直于地面，现要在其中两电线杆间的距离BC=7米．要在A、D间拉电线，则所拉电线最短为分析：从D点作AB的垂线，连接AD，可构成一个直角三角形，AD是直角三角形的斜边，根据勾股定理可求出AD的长．
解答：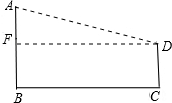
解：
作DF⊥AB于F，连接AD．
∵AB=4米，CD=2米，
∴AF=4-2=2米，
∵DF=BC=7米，
∴AD=
=3
．
则所拉电线最短为3
米．
解：作DF⊥AB于F，连接AD．
∵AB=4米，CD=2米，
∴AF=4-2=2米，
∵DF=BC=7米，
∴AD=
| 22+72 |
| 7 |
则所拉电线最短为3
| 7 |
点评：本题考查勾股定理的应用，和两点之间线段最短，根据题意把AD放在直角三角形中，从而可求出其长度．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
相关题目
的一侧，AB、CD、EF是三个标杆，相邻的两个标杆之间的距离都是2 m，已知AB、CD在灯光下的影长分别为BM=1.6 m，DN=0.6m．
如图两电线杆AB、CD都垂直于地面，现要在A、D间拉电线，则所拉电线最短为
如图两电线杆AB=4米，CD=2米，AB、CD都垂直于地面，现要在其中两电线杆间的距离BC=7米．要在A、D间拉电线，则所拉电线最短为________米．
如图两电线杆AB、CD都垂直于地面，现要在A、D间拉电线，则所拉电线最短为________米．其中AB=4米，CD=2米，两电线杆间的距离BC=6米．