题目内容
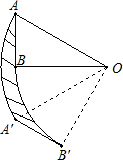 如图,将一个斜边长为2的三角板绕着它的30°角顶点逆时针旋转60°,那么,AB扫过的区域(图中阴影部分)的面积为
如图,将一个斜边长为2的三角板绕着它的30°角顶点逆时针旋转60°,那么,AB扫过的区域(图中阴影部分)的面积为| π |
| 6 |
| π |
| 6 |
分析:根据30°角所对的直角边等于斜边的一半求出AB的长度,再利用勾股定理求出BO的长,根据△ABO扫过的面积=S扇形AOA′+S△ABO,然后利用AB扫过的区域(图中阴影部分)的面积=△ABO扫过的面积-(S扇形BOB′+S△ABO),求出即可.
解答:解:如图所示,
∵∠AOB=30°,∠ABO=90°,AO=2,
∴BA=
AO=
×2=1,
BO=
=
=
,
∴△ABO扫过的面积=S扇形AOA′+S△ABO=
×22+
×1×
=
π+
,
则AB扫过的区域(图中阴影部分)的面积
=△ABO扫过的面积-(S扇形BOB′+S△ABO),
=
π+
-(
+
)
=
π-
=
故答案为:
.

∵∠AOB=30°,∠ABO=90°,AO=2,
∴BA=
| 1 |
| 2 |
| 1 |
| 2 |
BO=
| AO2-AB2 |
| 22-12 |
| 3 |
∴△ABO扫过的面积=S扇形AOA′+S△ABO=
| 60π |
| 360 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
则AB扫过的区域(图中阴影部分)的面积
=△ABO扫过的面积-(S扇形BOB′+S△ABO),
=
| 2 |
| 3 |
| 3 |
| 3 |
60π×(
| ||
| 360 |
=
| 2 |
| 3 |
| π |
| 2 |
=
| π |
| 6 |
故答案为:
| π |
| 6 |
点评:此题主要考查了旋转变换作图以及扇形的面积求解,勾股定理,30°角所对的直角边等于斜边的一半的性质,找出对应点的位置是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
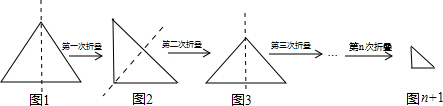
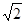 的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠
的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠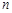 次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).
次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).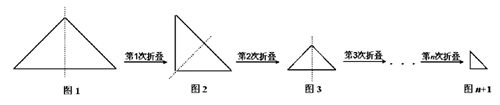
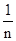
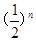
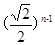
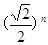
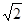 的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠
的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到另一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到又一个等腰直角三角形(如图3),若连续将图1的等腰直角三角形折叠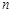 次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).
次后所得到的等腰直角三角形(如图n+1)的斜边长为( * ).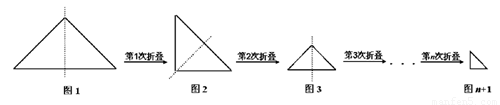
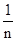 (B)
(B)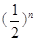 (C)
(C)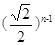 (D)
(D)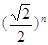
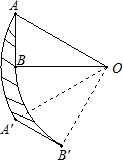 如图,将一个斜边长为2的三角板绕着它的30°角顶点逆时针旋转60°,那么,AB扫过的区域(图中阴影部分)的面积为________.
如图,将一个斜边长为2的三角板绕着它的30°角顶点逆时针旋转60°,那么,AB扫过的区域(图中阴影部分)的面积为________.