题目内容
已知m、n是有理数，方程x2+mx+n=0有一根是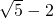
，求m+n的值．
解：∵方程x2+mx+n=0中有一个根是
-2，
∴
+m（-2）+n=0，
即9-2m+n=（4-m），
又m、n均为有理数，
∴m-4=0
解得：m=4，
所以9-2×4+n=0
解得n=-1，∴m+n=3．
故答案为：3．
分析：将方程的一个根代入方程，得到一个代数式，根据m、n均为有理数可得到m的值，从而得到n的值．
点评：本题主要考查了根与系数的关系，难度适中，关键是将已知根代入后根据m、n是有理数解题．
-2，∴
+m（-2）+n=0，即9-2m+n=（4-m）
，又m、n均为有理数，
∴m-4=0
解得：m=4，
所以9-2×4+n=0
解得n=-1，∴m+n=3．
故答案为：3．
分析：将方程的一个根代入方程，得到一个代数式，根据m、n均为有理数可得到m的值，从而得到n的值．
点评：本题主要考查了根与系数的关系，难度适中，关键是将已知根代入后根据m、n是有理数解题．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
已知a、b是有理数，观察下表中的运算，并在空格内填上相应的数．
| a与b的运算 | a+2b | 2a+b |
| ||
| 运算的结果 | 2 | 4 |