Question

在Rt△ABC中，∠C=90°，AB=5，AC=4，△ABC绕点A旋转后点C落在AB边上，点B落在点B′，那么BB′的长为________．

Answer 1

分析：如图，根据题意，△ABC绕点A旋转后得到△AB′C′，可得，AC′=4，AB′=5，B′C′=3，BC′=1，所以，在Rt△B′C′B中，应用勾股定理，即可求得．
解答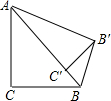：解：如图，∵△ABC绕点A旋转后得到△AB′C′，
∴△ABC≌△AB′C′，
∵∠C=90°，AB=5，AC=4，
∴∠AC′B′=∠B′C′B=90°，AC′=4，AB′=5，
∴B′C′=3，BC′=1，
∴在Rt△B′C′B中，
BB′===．
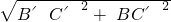故答案为：．
点评：本题主要考查了勾股定理和旋转的性质，知道旋转前后的两个图形完全相等，是解答本题的基础；并能熟练应用勾股定理求值．