题目内容
 (2013•本溪一模)如图,把一个含有30°角的直角三角板ABC如图放置,把三角板绕点A顺时针旋转30°后,到三角形AB′C′的位置,若AB=4,图中阴影部分的面积为
(2013•本溪一模)如图,把一个含有30°角的直角三角板ABC如图放置,把三角板绕点A顺时针旋转30°后,到三角形AB′C′的位置,若AB=4,图中阴影部分的面积为| 4π |
| 3 |
| 4π |
| 3 |
分析:首先求出直角三角板ABC斜边上的高,进而得出S△C′B′C,再利用扇形面积减去△ABC面积,进而得出答案.
解答: 解:过点C′作C′D⊥AB′于点D,
解:过点C′作C′D⊥AB′于点D,
由题意得出:∠C′AB′=∠BAB′=30°,AB=AB′=4,
∴AC′=4×cos30°=2
,
∴C′D=
,
∴B′C=AB′-AC=4-2
,
∴S△C′B′C=
×B′C×C′D=
×(4-2
)×
=2
-3,
S阴影BB′C=S扇形BAB′-S△ABC=
-
×
×4=
-2
,
∴图中阴影部分的面积为:2
-3+
-2
=
-3.
故答案为:
-3.
 解:过点C′作C′D⊥AB′于点D,
解:过点C′作C′D⊥AB′于点D,由题意得出:∠C′AB′=∠BAB′=30°,AB=AB′=4,
∴AC′=4×cos30°=2
| 3 |
∴C′D=
| 3 |
∴B′C=AB′-AC=4-2
| 3 |
∴S△C′B′C=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
S阴影BB′C=S扇形BAB′-S△ABC=
| 30π×42 |
| 360 |
| 1 |
| 2 |
| 3 |
| 4π |
| 3 |
| 3 |
∴图中阴影部分的面积为:2
| 3 |
| 4π |
| 3 |
| 3 |
| 4π |
| 3 |
故答案为:
| 4π |
| 3 |
点评:此题主要考查了扇形面积公式以及三角形面积求法等知识,根据已知分割阴影部分得出是解题关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
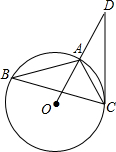 (2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.
(2013•本溪一模)如图,已知:△ABC是的⊙O内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°.

 (2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.
(2013•本溪一模)如图,已知抛物线y=ax2+bx+3(a≠0)经过A(-1,0),C(3,0)两点.