题目内容
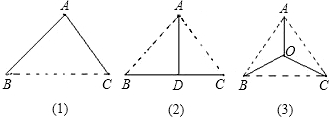
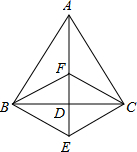
 若△ABC是边长为6的等边三角形,点F是△ABC的重心,连接AF延长至点E,交BC于D,CF∥BE,则四边形BECF的周长为________.
若△ABC是边长为6的等边三角形,点F是△ABC的重心,连接AF延长至点E,交BC于D,CF∥BE,则四边形BECF的周长为________.
8
分析:根据等边三角形的性质可知外心,重心,垂心三心合一;且内角均为60°;根据勾股定理可求出AD的长,利用重心的性质可求出DF的长,再证明四边形BECF是菱形即可求出其周长.
解答:∵△ABC是边长为6的等边三角形,点F是△ABC的重心,
∴AB=BC=6,AD⊥BC,
∴BD=CD= BC=3,
BC=3,
∴AD=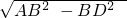 =3
=3 ,
,
∴FD= AD=
AD= ,
,
∵AD⊥BC,BD=CD,
∴BF=CF,BE=CE,
∴∠BEF=∠CEF,
∵CF∥BE,
∴∠CFE=∠BEF,
∴∠CEF=∠CFE,
∴CF=CE,
∴BE=CE=CF=BF,
∴四边形BECF是菱形,
∵BD=3,DF= ,
,
∴BF=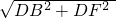 =2
=2 ,
,
∴四边形BECF的周长是4×2 =8
=8 .
.
故答案为:8 .
.
点评:本题考查了等边三角形的性质、重心的性质、勾股定理的运用以及菱形的判定和性质,题目的综合性很强,难度不大.

分析:根据等边三角形的性质可知外心,重心,垂心三心合一;且内角均为60°;根据勾股定理可求出AD的长,利用重心的性质可求出DF的长,再证明四边形BECF是菱形即可求出其周长.
解答:∵△ABC是边长为6的等边三角形,点F是△ABC的重心,
∴AB=BC=6,AD⊥BC,
∴BD=CD=
 BC=3,
BC=3,∴AD=
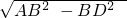 =3
=3 ,
,
∴FD=
 AD=
AD= ,
,∵AD⊥BC,BD=CD,
∴BF=CF,BE=CE,
∴∠BEF=∠CEF,
∵CF∥BE,
∴∠CFE=∠BEF,
∴∠CEF=∠CFE,
∴CF=CE,
∴BE=CE=CF=BF,
∴四边形BECF是菱形,
∵BD=3,DF=
 ,
,∴BF=
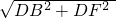 =2
=2 ,
,∴四边形BECF的周长是4×2
 =8
=8 .
.故答案为:8
 .
.点评:本题考查了等边三角形的性质、重心的性质、勾股定理的运用以及菱形的判定和性质,题目的综合性很强,难度不大.

练习册系列答案
相关题目
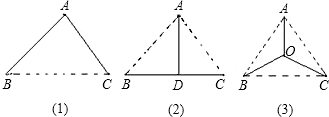
 如图,△ABC是等边三角形,
如图,△ABC是等边三角形, 若△ABC是边长为6的等边三角形,点F是△ABC的重心,连接AF延长至点E,交BC于D,CF∥BE,则四边形BECF的周长为
若△ABC是边长为6的等边三角形,点F是△ABC的重心,连接AF延长至点E,交BC于D,CF∥BE,则四边形BECF的周长为 ≈1.141,
≈1.141,