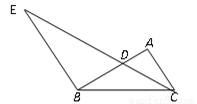
题目内容
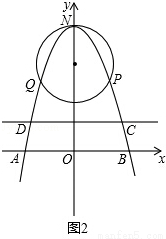
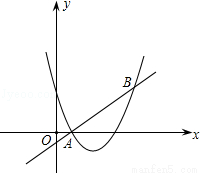
已知过原点O的两直线与圆心为M(0,4),半径为2的圆相切,切点分别为P、Q,PQ交y轴于点K,抛物线经过P、Q两点,顶点为N(0,6),且与x轴交于A、B两点.

(1)求点P的坐标;
(2)求抛物线解析式;
(3)在直线y=nx+m中,当n=0,m≠0时,y=m是平行于x轴的直线,设直线y=m与抛物线相交于点C、D,当该直线与⊙M相切时,求点A、B、C、D围成的多边形的面积(结果保留根号).
(1)点P的坐标为(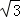 ,3) (2)
,3) (2)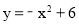 (3)4+2
(3)4+2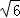 或6
或6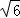
【解析】
试题分析:(1)由切线的性质可得∠MPO=90°,根据勾股定理可求出PO,然后由面积法可求出PK,然后运用勾股定理可求出OK,就可得到点P的坐标;
(2)可设顶点为(0,6)的抛物线的解析式为y=ax2+6,然后将点P的坐标代入就可求出抛物线的解析式;(3)直线y=m与⊙M相切有两种可能,只需对这两种情况分别讨论就可求出对应多边形的面积.
试题解析:【解析】
(1)如图1,
∵⊙M与OP相切于点P,
∴MP⊥OP,即∠MPO=90°.
∵点M(0,4)即OM=4,MP=2,
∴OP=2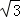 .
.
∵⊙M与OP相切于点P,⊙M与OQ相切于点Q,
∴OQ=OP,∠POK=∠QOK.
∴OK⊥PQ,QK=PK.
∴PK=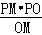 =
=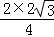 =
=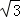 .
.
∴OK=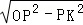 =3.
=3.
∴点P的坐标为(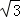 ,3).
,3).
(2)如图2,
设顶点为(0,6)的抛物线的解析式为y=ax2+6,
∵点P(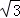 ,3)在抛物线y=ax2+6上,
,3)在抛物线y=ax2+6上,
∴3a+6=3.
解得:a=﹣1.
则该抛物线的解析式为y=﹣x2+6.
(3)当直线y=m与⊙M相切时,
则有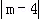 =2.
=2.
解得;m1=2,m2=6.
①m=2时,如图3,
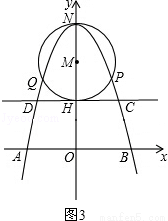
则有OH=2.
当y=2时,解方程﹣x2+6=2得:x=±2,
则点C(2,2),D(﹣2,2),CD=4.
同理可得:AB=2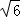 .
.
则S梯形ABCD= (DC+AB)•OH=
(DC+AB)•OH= (4+2
(4+2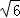 )×2=4+2
)×2=4+2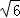 .
.
②m=6时,如图4,
此时点C、点D与点N重合.
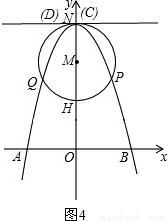
S△ABC=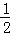 AB•OC=
AB•OC=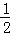 ×2
×2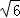 ×6=6
×6=6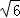 .
.
综上所述:点A、B、C、D围成的多边形的面积为4+2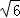 或6
或6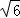
考点:切线的性质,勾股定理,二次函数的图像与性质,梯形及三角形的面积

 口算题天天练系列答案
口算题天天练系列答案 ,相应算式是( )
,相应算式是( ) ×5﹣0×5÷2= B.(
×5﹣0×5÷2= B.( ﹣0•5÷2= D.(
﹣0•5÷2= D.( =0•5)÷2=
=0•5)÷2=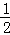 ,﹣2中,最小的一个实数是( )
,﹣2中,最小的一个实数是( ) 、
、 为两个连续的整数,且
为两个连续的整数,且 <
< <
< ,则
,则 = .
= . 的长等于( )
的长等于( ) B.
B. C.
C. D.
D.
 +kx+b经过点P(2,-3),Q(-1,0).
+kx+b经过点P(2,-3),Q(-1,0).
 ,与
,与 轴交点为
轴交点为 .求
.求 的值.
的值. 轴的另一个交点为
轴的另一个交点为 ,求四边形
,求四边形 的面积.
的面积. ,AB=10,则AC的长为
,AB=10,则AC的长为