题目内容
如图,点A、B、C在一直线上,则图中共有射线( )
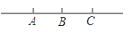
A. 1条 B. 2条 C. 4条 D. 6条
D 【解析】【解析】 根据射线的定义,这条直线上的每个点可以有两条射线,故图中共有射线6条.故选D.
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
题目内容
如图,点A、B、C在一直线上,则图中共有射线( )
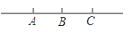
A. 1条 B. 2条 C. 4条 D. 6条
D 【解析】【解析】 根据射线的定义,这条直线上的每个点可以有两条射线,故图中共有射线6条.故选D. 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案