题目内容
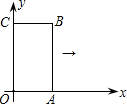 (2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
(2012•绍兴)如图,矩形OABC的两条边在坐标轴上,OA=1,OC=2,现将此矩形向右平移,每次平移1个单位,若第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
分析:可设反比例函数解析式为y=
,根据第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,可分两种情况:①与BC,AB平移后的对应边相交;②与OC,AB平移后的对应边相交;得到方程求得反比例函数解析式,再代入第n次(n>1)平移的横坐标得到矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值.
| k |
| x |
解答: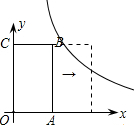 解:设反比例函数解析式为y=
解:设反比例函数解析式为y=
,则
①与BC,AB平移后的对应边相交;
与AB平移后的对应边相交的交点的坐标为(2,1.4),
则1.4=
,
解得k=2.8=
,
故反比例函数解析式为y=
.
则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为:
-
=
;
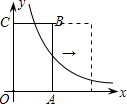 ②与OC,AB平移后的对应边相交;
②与OC,AB平移后的对应边相交;
k-
=0.6,
解得k=
.
故反比例函数解析式为y=
.
则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为:
-
=
.
故第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
或
.
故答案为:
或
.
 解:设反比例函数解析式为y=
解:设反比例函数解析式为y=| k |
| x |
①与BC,AB平移后的对应边相交;
与AB平移后的对应边相交的交点的坐标为(2,1.4),
则1.4=
| k |
| 2 |
解得k=2.8=
| 14 |
| 5 |
故反比例函数解析式为y=
| 14 |
| 5x |
则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为:
| 14 |
| 5n |
| 14 |
| 5(n+1) |
| 14 |
| 5n(n+1) |
 ②与OC,AB平移后的对应边相交;
②与OC,AB平移后的对应边相交;k-
| k |
| 2 |
解得k=
| 6 |
| 5 |
故反比例函数解析式为y=
| 6 |
| 5x |
则第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为:
| 6 |
| 5n |
| 6 |
| 5(n+1) |
| 6 |
| 5n(n+1) |
故第n次(n>1)平移得到的矩形的边与该反比例函数图象的两个交点的纵坐标之差的绝对值为
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
故答案为:
| 14 |
| 5n(n+1) |
| 6 |
| 5n(n+1) |
点评:考查了反比例函数综合题,本题的关键是根据第1次平移得到的矩形的边与反比例函数图象有两个交点,它们的纵坐标之差的绝对值为0.6,分①与BC,AB平移后的对应边相交;②与OC,AB平移后的对应边相交;两种情况讨论求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
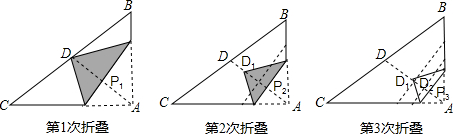
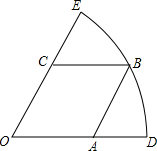 (2012•绍兴)如图,扇形DOE的半径为3,边长为
(2012•绍兴)如图,扇形DOE的半径为3,边长为
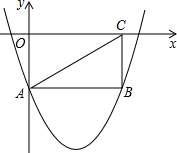 (2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(2012•绍兴)如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.