题目内容
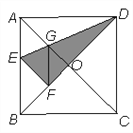
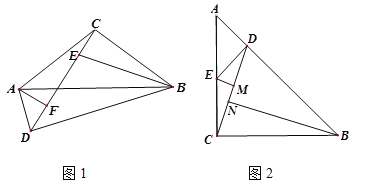
【题目】小明在学习过程中遇到这样一个问题:如图1,在△ABC中,CA=CB,E是CD上一点,且ED=EB, ∠DEB=∠ACB,连接AD,探究∠ADC与∠DCB之间的数量关系.小明发现,∠ACD=∠CBE,CA=CB,因此可以通过作∠CAF=∠BCE交CD于点F构造全等,经过推理论证解决问题.
(1)按照小明思考问题的方法,解决问题;
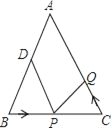
(2)如图2,∠ACB=90,CA=CB,D是AB上一点,过点D作DE⊥AB交AC于点E,过点E作EM⊥CD于点M,BN⊥CD于点N,探究EM,BN,CD之间的数量关系.
【答案】(1)∠DCB=2∠ADC,证明详见解析;(2)BN= CD+EM,理由详见解析.
【解析】
(1)∠DCB=2∠ADC,作∠CAF=∠BCE交CD于点F,证明△ACF≌△CBE,根据全等三角形的性质可得AF=CE,CF=BE,∠AFC=∠DCB,再证得AF=DF,根据等腰三角形的性质可得∠ADF=∠DAF,由三角形外角的性质即可证得结论;(2)BN= CD+EM,过点A作AH⊥CD交CD的延长线于点H(如图2),先证得Rt△ACH≌Rt△CBN,根据全等三角形的性质可得CH=BN,再证得Rt△ADH≌Rt△DEM,根据全等三角形的性质可得EM=DH,由BN= CD+DH= CD+EM.即可证得结论.
(1)∠DCB=2∠ADC,理由如下,
如图1,作∠CAF=∠BCE交CD于点F,

∵∠DEB=∠EBC+∠ECB,∠ACB=∠ACF+∠ECB,∠DEB=∠ACB,
∴∠ACF=∠CBE,
在△ACF和△CBE中,
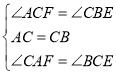
∴△ACF≌△CBE,
∴AF=CE,CF=BE,∠AFC=∠DCB,
∵DE=EB,
∴DE=CF,
∴DF=CE,
∵AF=CE,
∴AF=DF,
∴∠ADF=∠DAF,
∴∠AFC=∠ADF+∠DAF=2∠ADC,
∵∠AFC=∠DCB,
∴∠DCB=2∠ADC.
(2)BN= CD+EM,理由如下:
过点A作AH⊥CD交CD的延长线于点H(如图2),
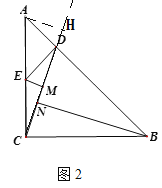
∵AH⊥CD,BN⊥CD,
∴∠AHC=∠CNB=90°,
∴∠CBN+∠NCB=90°,
∵∠ACH+∠NCB=90°,
∴∠CBN=∠ACH,
在Rt△ACH和Rt△CBN中,
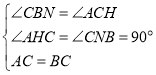 ,
,
∴Rt△ACH≌Rt△CBN,
∴CH=BN,
∵∠ACB=90,CA=CB,
∴∠EDA=45°,
∵DE⊥AB,
∴△AED为等腰直角三角形,
∴AD=DE,
∵AH⊥CD,EM⊥CD,
∴∠AHD=∠DME=90°,
∴∠DAH+∠ADH=90°,
∵∠ADH+∠EDM=90°,
∴∠DAH=∠EDM,
在Rt△ADH和Rt△DEM中,
 ,
,
∴Rt△ADH≌Rt△DEM,
∴EM=DH,
∵CH=CD+DH,CH=BN,
∴BN= CD+DH= CD+EM.

 阅读快车系列答案
阅读快车系列答案【题目】“十一”黄金周期间,重庆仙女山风景区7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.2 | +0.4 | +0.8 | ﹣0.4 | ﹣0.8 | +0.2 | ﹣1.2 |
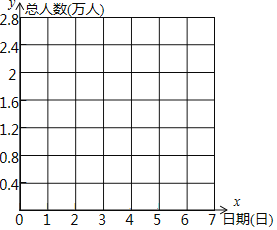
(1)若9月30日的游客人数记为a,请用含a的式子表示10月5日的游客人数: 万人.
(2)判断七天内游客人数最多的是 日,最少的是 日.
(3)以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数情况:人数变化(万人)