题目内容
(8分)如图,在△ABC中,AB=17,BC=16,BC边上的中线AD=15,

(1)求AC;
(2)若点P在边AC上移动,则BP的最小值是 .
证明 ,AC=17,高=
,AC=17,高=
【解析】
试题分析:(1)根据BC=16,BC边上的中线AD=15,得BD=8,又AB=17,由勾股定理的逆定理可得 ,在△ADC中,由勾股定理可得AC=17;(2)点P在边AC上移动,则当BP是高时,BP的最小值,根据面积可求BP的值.
,在△ADC中,由勾股定理可得AC=17;(2)点P在边AC上移动,则当BP是高时,BP的最小值,根据面积可求BP的值.
试题解析:(1)因为BC=16,BC边上的中线AD=15,所以BD=8,又AB=17,在△ABD中,因为 ,所以
,所以 ,所以
,所以 ,所以在△ADC中,
,所以在△ADC中, ,所以
,所以 ;(2)因为点P在边AC上移动,所以当BP是高时,BP的值最小,因为
;(2)因为点P在边AC上移动,所以当BP是高时,BP的值最小,因为 所以
所以 所以BP=
所以BP= .
.
考点:1.勾股定理的逆定理;2.勾股定理.

练习册系列答案
相关题目



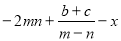 的值.
的值.