题目内容
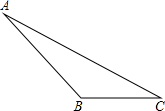 如图,已知一钝角△ABC中,BC=2
如图,已知一钝角△ABC中,BC=2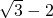 ,∠C=30°,BC边上的高为2.试求:
,∠C=30°,BC边上的高为2.试求:
(1)AB的长.
(2)∠BAC的度数.
(3)△ABC内切圆的半径.(结果精确到0.01)

解:(1)过A作AD⊥BC,交CB延长线于D,
∵∠C=30°,BC边上的高AD为2
∴AC=2AD=4,
由勾股定理得:DC=
 =2
=2 ,
,∴DB=DC-BC=2
 -(2
-(2 -2)=2=AD,
-2)=2=AD,由勾股定理得:AB=
 =2
=2 ;
;(2)∵AD=DB=2,
∴∠DAB=∠ABD,
∵∠D=90°,
即∠DAB=∠ABD=45°,
∴∠ABC=180°-45°=135°;
(3)

∵∠D=90°,∠C=30°,AD=2,
∴AC=2AD=4,
设⊙O的半径是r,
则由三角形面积公式得:
 ×BC×AD=
×BC×AD= ×(AB+BC+AC)r,
×(AB+BC+AC)r,r=
 =
= ≈0.35,
≈0.35,即⊙O的半径约为0.35.
分析:(1)过A作AD⊥BC,交CB延长线于D,求出AD,求出BD,根据勾股定理求出AB即可;
(2)根据AD=BD可求出∠ABD=45°,求出即可;
(2)设设⊙O的半径是r,由三角形面积公式得:
 ×BC×AD=
×BC×AD= ×(AB+BC+AC)r,求出即可.
×(AB+BC+AC)r,求出即可.点评:本题考查了含30度角的直角三角形性质,勾股定理,等腰三角形的性质和判定,三角形的内切圆等知识点的应用,主要考查学生综合运用定理进行计算和推理的能力.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 (2013•金山区一模)如图,已知一钝角△ABC中,BC=2
(2013•金山区一模)如图,已知一钝角△ABC中,BC=2
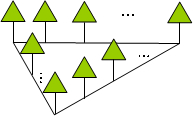 某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生一齐动手,在空地的三条边上栽上了树苗(如图).已知三边上的树苗数分别为50、14、48,空地的三个角均有一棵树,且每条边上的树苗株距均为1米,那么这块空地的形状为( )
某中学旁边有一块三角形空地,为了保持水土,美化环境,全校师生一齐动手,在空地的三条边上栽上了树苗(如图).已知三边上的树苗数分别为50、14、48,空地的三个角均有一棵树,且每条边上的树苗株距均为1米,那么这块空地的形状为( )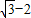 ,∠C=30°,BC边上的高为2.试求:
,∠C=30°,BC边上的高为2.试求: