题目内容
已知二次函数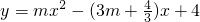 的图象与x轴交于点A,B,与y轴交于点C,若△ABC是等腰三角形,求这个二次函数的解析式.
的图象与x轴交于点A,B,与y轴交于点C,若△ABC是等腰三角形,求这个二次函数的解析式.
解:令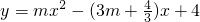 =0,则可得出A(3,0)、B(
=0,则可得出A(3,0)、B( ,0);
,0);
再令x=0,y=4,则可得出C点坐标为(0,4).
由于△ABC是等腰三角形,则分以下三种情况讨论:
(1)若AC=BC,则 =-3,m=
=-3,m=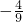 ,所求二次函数的解析式为y=
,所求二次函数的解析式为y=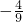 x2+4;
x2+4;
(2)若AB=AC,则|3- |=|AC|=5,则m=
|=|AC|=5,则m= 或
或 ,所求二次函数的解析式为y=
,所求二次函数的解析式为y= x2+
x2+ x+4或y=
x+4或y= x2-
x2- x+4;
x+4;
(3)若AB=BC,则AC的中垂线与x轴的交点即为B点,求出AC的中垂线为:y= x+
x+ ,再令y=0,x=
,再令y=0,x= ,即
,即 =
= ,m=
,m= ,所求二次函数的解析式为y=
,所求二次函数的解析式为y= x2+
x2+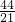 x+4.
x+4.
分析:由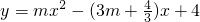 求出A、B、C三点坐标,再分情况讨论:①AC=BC;②AB=AC;③AB=BC分别满足时m的取值,求得二次函数的解析式.
求出A、B、C三点坐标,再分情况讨论:①AC=BC;②AB=AC;③AB=BC分别满足时m的取值,求得二次函数的解析式.
点评:本题考查了数形结合的思想,由等腰三角形的两腰相等确定点的坐标,再求解析式里的未知量,确定函数解析式.
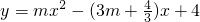 =0,则可得出A(3,0)、B(
=0,则可得出A(3,0)、B( ,0);
,0);再令x=0,y=4,则可得出C点坐标为(0,4).
由于△ABC是等腰三角形,则分以下三种情况讨论:
(1)若AC=BC,则
 =-3,m=
=-3,m=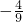 ,所求二次函数的解析式为y=
,所求二次函数的解析式为y=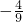 x2+4;
x2+4;(2)若AB=AC,则|3-
 |=|AC|=5,则m=
|=|AC|=5,则m= 或
或 ,所求二次函数的解析式为y=
,所求二次函数的解析式为y= x2+
x2+ x+4或y=
x+4或y= x2-
x2- x+4;
x+4;(3)若AB=BC,则AC的中垂线与x轴的交点即为B点,求出AC的中垂线为:y=
 x+
x+ ,再令y=0,x=
,再令y=0,x= ,即
,即 =
= ,m=
,m= ,所求二次函数的解析式为y=
,所求二次函数的解析式为y= x2+
x2+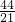 x+4.
x+4.分析:由
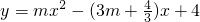 求出A、B、C三点坐标,再分情况讨论:①AC=BC;②AB=AC;③AB=BC分别满足时m的取值,求得二次函数的解析式.
求出A、B、C三点坐标,再分情况讨论:①AC=BC;②AB=AC;③AB=BC分别满足时m的取值,求得二次函数的解析式.点评:本题考查了数形结合的思想,由等腰三角形的两腰相等确定点的坐标,再求解析式里的未知量,确定函数解析式.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
已知二次函数的图象与y轴的交点坐标为(0,a),与x轴的交点坐标为(b,0)和(-b,0),若a>0,则函数解析式为( )
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
 已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.
已知二次函数的图象与x轴交于点A(-1,0)和点B(3,0),且与直线y=kx-4交y轴于点C.