题目内容
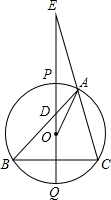 (1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE.
(1998•南京)已知:如图,△ABC内接于⊙O,过圆心O作BC的垂线交⊙O于点P、Q,交AB于点D,QP、CA的延长线交于点E.求证:OA2=OD•OE.分析:作直径AM,连接BM,求出∠E=∠DAO,公共角∠DOA=∠DOA,推出△DOA∽△AOE,得出比例式,即可得出答案.
解答:证明: 作直径AM,连接BM,
作直径AM,连接BM,
∵∠C和∠M都对弧AB,
∴∠C=∠M,
∵OQ⊥BC,
∴∠EQC=90°,
∴∠C+∠E=90°,
∵AM为⊙O直径,
∴∠ABM=90°,
∴∠M+∠OAD=90°,
∴∠E=∠OAD,
∵∠DOA=∠DOA,
∴△DOA∽△AOE,
∴
=
,
即OA2=OD•OE.
 作直径AM,连接BM,
作直径AM,连接BM,∵∠C和∠M都对弧AB,
∴∠C=∠M,
∵OQ⊥BC,
∴∠EQC=90°,
∴∠C+∠E=90°,
∵AM为⊙O直径,
∴∠ABM=90°,
∴∠M+∠OAD=90°,
∴∠E=∠OAD,
∵∠DOA=∠DOA,
∴△DOA∽△AOE,
∴
| OA |
| OD |
| OE |
| OA |
即OA2=OD•OE.
点评:本题考查了圆周角定理和相似三角形的性质和判定的应用,注意:直径所对的圆周角是直角,相似三角形的对应边的比相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
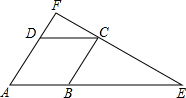 (1998•南京)已知:如图,菱形ABCD的边长为3,延长AB到点E,使BE=2AB,连接EC并延长交AD的延长线于点F.求AF的长.
(1998•南京)已知:如图,菱形ABCD的边长为3,延长AB到点E,使BE=2AB,连接EC并延长交AD的延长线于点F.求AF的长. (1998•南京)已知:如图,点P在∠AOB的边OA上.
(1998•南京)已知:如图,点P在∠AOB的边OA上.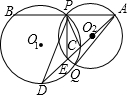 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且