题目内容
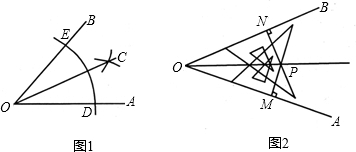
阅读材料,解答问题.材料:“小聪设计的一个电子游戏是:一电子跳蚤从这P1(-3,9)开始,按点的横坐标依次增加1的规律,在抛物线y=x2上向右跳动,得到点P2、P3、P4、P5…(如图1所示).过P1、P2、P3分别作P1H1、P2H2、P3H3垂直于x轴,垂足为H1、H2、H3,则S△P1P2P3=S梯形P1H1H3P3-S梯形P1H1H2P2-S梯形P2H2H3P3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
问题:
(1)求四边形P1P2P3P4和P2P3P4P5的面积(要求:写出其中一个四边形面积的求解过程,另一个直接写出答案);
(2)猜想四边形Pn-1PnPn+1Pn+2的面积,并说明理由(利用图2);
(3)若将抛物线y=x2改为抛物线y=x2+bx+c,其它条件不变,猜想四边形Pn-1PnPn+1Pn+2的面积(直接写出答案).

分析:(1)作P5H5垂直于x轴,垂足为H5,把四边形P1P2P3P4和四边形P2P3P4P5的转化为SP1P2P3P4=S△OP1H1-S△OP3H3-S梯形P2H2H3P3-S梯形P1H1H2P2和SP2P3P4P5=S梯形P5H5H2P2-S△P5H5O-S△OH3P3-S梯形P2H2H3P3来求解;
(2)(3)由图可知,Pn-1、Pn、Pn+1、Pn+2的横坐标为n-5,n-4,n-3,n-2,代入二次函数解析式,
可得Pn-1、Pn、Pn+1、Pn+2的纵坐标为(n-5)2,(n-4)2,(n-3)2,(n-2)2,将四边形面积转化为S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2来解答.
(2)(3)由图可知,Pn-1、Pn、Pn+1、Pn+2的横坐标为n-5,n-4,n-3,n-2,代入二次函数解析式,
可得Pn-1、Pn、Pn+1、Pn+2的纵坐标为(n-5)2,(n-4)2,(n-3)2,(n-2)2,将四边形面积转化为S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2来解答.
解答:解:(1)作P5H5垂直于x轴,垂足为H5,
由图可知SP1P2P3P4=S△OP1H1-S△OP3H3-S梯形P2H2H3P3-S梯形P1H1H2P2=
-
-
-
=4,
SP2P3P4P5=S梯形P5H5H2P2-S△P5H5O-S△OH3P3-S梯形P2H2H3P3=
-
-
-
=4;
(2)作Pn-1Hn-1、PnHn、Pn+1Hn+1、Pn+2Hn+2垂直于x轴,垂足为Hn-1、Hn、Hn+1、Hn+2,
由图可知Pn-1、Pn、Pn+1、Pn+2的横坐标为n-5,n-4,n-3,n-2,
代入二次函数解析式,可得Pn-1、Pn、Pn+1、Pn+2的纵坐标为(n-5)2,(n-4)2,(n-3)2,(n-2)2,
四边形Pn-1PnPn+1Pn+2的面积为S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2=
-
-
-
=4;
(3)S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2=
-
-
-
=4.
由图可知SP1P2P3P4=S△OP1H1-S△OP3H3-S梯形P2H2H3P3-S梯形P1H1H2P2=
| 9×3 |
| 2 |
| 1×1 |
| 2 |
| 1+4 |
| 2 |
| 4+9 |
| 2 |
SP2P3P4P5=S梯形P5H5H2P2-S△P5H5O-S△OH3P3-S梯形P2H2H3P3=
| 3(1+4) |
| 2 |
| 1×1 |
| 2 |
| 1×1 |
| 2 |
| 1+4 |
| 2 |
(2)作Pn-1Hn-1、PnHn、Pn+1Hn+1、Pn+2Hn+2垂直于x轴,垂足为Hn-1、Hn、Hn+1、Hn+2,
由图可知Pn-1、Pn、Pn+1、Pn+2的横坐标为n-5,n-4,n-3,n-2,
代入二次函数解析式,可得Pn-1、Pn、Pn+1、Pn+2的纵坐标为(n-5)2,(n-4)2,(n-3)2,(n-2)2,
四边形Pn-1PnPn+1Pn+2的面积为S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2=
| 3[(n-5)2+(n-2)2] |
| 2 |
| (n-5)2+(n-4)2 |
| 2 |
| (n-4)2+(n-3)2 |
| 2 |
| (n-3)2+(n-2)2 |
| 2 |
(3)S四边形Pn-1PnPn+1Pn+2=S梯形Pn-5Hn-5Hn-2Pn-2-S梯形Pn-5Hn-5Hn-4Pn-4-S梯形Pn-4Hn-4Hn-3Pn-3-S梯形Pn-3Hn-3Hn-2Pn-2=
| 3[(n-5)2+b(n-5)+c+(n-2)2+b(n-2)+c] |
| 2 |
| (n-5)2+b(n-5)+c+(n-4)2+b(n-4)+c |
| 2 |
| (n-4)2+b(n-4)+c+(n-3)2+b(n-3)+c |
| 2 |
| (n-3)2+b(n-3)+c+(n-2)2+b(n-2)+c |
| 2 |
点评:此题是一道材料分析题,考查了根据函数坐标特点求图形面积的知识.
解答时要注意,前一小题为后面的题提供思路,由于计算量极大,要仔细计算,以免出错,
解答时要注意,前一小题为后面的题提供思路,由于计算量极大,要仔细计算,以免出错,

练习册系列答案
相关题目
 24、阅读材料,解答问题.
24、阅读材料,解答问题.