题目内容
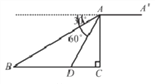
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
【答案】(1)120米;(2) ![]()
【解析】试题分析:(1)、根据题意得出∠ABD=30°,则根据Rt△ABC中∠ABD的正弦值得出AB的长度;(2)、过A′作A′E⊥BC交BC的延长线于E,连接A′D,根据题意得出A′E,CE的长度,然后根据Rt△ADC的性质得出DC的长度,从而得出DE的长度,最后根据tan∠AA′D=tan∠A′DC=![]() 得出答案.
得出答案.
试题解析:解:(1)由题意得:∠ABD=30°,∠ADC=60°,
在Rt△ABC中,AC=60m, ∴AB= ;
;
(2)过A′作A′E⊥BC交BC的延长线于E,连接A′D,

则A′E=AC=60, CE=AA′=![]() ,
,
在Rt△ADC中, AC=60m, ∠ADC=60°, ∵DC=![]() , ∴DE=
, ∴DE=![]() ,
,
∴tan∠AA′D=tan∠A′DC=![]() .
.
答:从无人机A′上看目标D的俯角的正切值是![]() .
.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目