题目内容
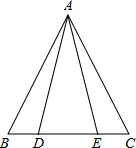 如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形________(写出一对即可).
如图.点D、E在△ABC的边BC上,AB=AC,AD=AE.请写出图中的全等三角形________(写出一对即可).
△ABD≌△ACE(答案不唯一)
分析:根据等边对等角的性质可得∠B=∠C,∠ADE=∠AED,再根据等角的补角相等可得∠ADB=∠AEC,然后根据“角角边”即可得到全等三角形.
解答:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC,
在△ABD和△ACE中,
∵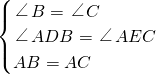 ,
,
∴△ABD≌△ACE(AAS),
在△ABE和△ACD中,
∵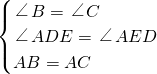 ,
,
∴△ABE≌△ACD(AAS).
故答案为:△ABD≌△ACE(答案不唯一).
点评:本题考查了全等三角形的判定与性质,等腰三角形的性质,根据等边对等角的性质得到相等的角是解题的关键.
分析:根据等边对等角的性质可得∠B=∠C,∠ADE=∠AED,再根据等角的补角相等可得∠ADB=∠AEC,然后根据“角角边”即可得到全等三角形.
解答:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC,
在△ABD和△ACE中,
∵
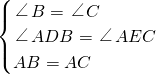 ,
,∴△ABD≌△ACE(AAS),
在△ABE和△ACD中,
∵
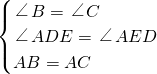 ,
,∴△ABE≌△ACD(AAS).
故答案为:△ABD≌△ACE(答案不唯一).
点评:本题考查了全等三角形的判定与性质,等腰三角形的性质,根据等边对等角的性质得到相等的角是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目


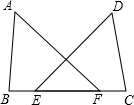 如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
 如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为
如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为