题目内容
（2012•绵阳）图（1）是一个长为2m，宽为2n（m＞n）的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图（2）那样拼成一个正方形，则中间空的部分的面积是（ ）分析：先求出正方形的边长，继而得出面积，然后根据空白部分的面积=正方形的面积-矩形的面积即可得出答案．
解答：解：由题意可得，正方形的边长为（m+n），
故正方形的面积为（m+n）2，
又∵原矩形的面积为4mn，
∴中间空的部分的面积=（m+n）2-4mn=（m-n）2．
故选C．
故正方形的面积为（m+n）2，
又∵原矩形的面积为4mn，
∴中间空的部分的面积=（m+n）2-4mn=（m-n）2．
故选C．
点评：此题考查了完全平方公式的几何背景，求出正方形的边长是解答本题的关键，难度一般．
练习册系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
（2012•绵阳）如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，已知∠AP′B=135°，P′A：P′C=1：3，则P′A：PB=（ ）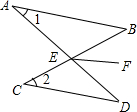
（2012•绵阳）如图，AB∥CD，AD与BC交于点E，EF是∠BED的平分线，若∠1=30°，∠2=40°，则∠BEF=
（2012•绵阳）如图，正方形的边长为2，以各边为直径在正方形内画半圆，则图中阴影部分的面积为