题目内容
有三组数x1，x2，x3；y1，y2，y3；z1，z2，z3，它们的平均数分别是a，b，c，那么x1+y1-z1，x2+y2-z2，x3+y3-z3的平均数是
- A.
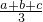
- B.
- C.a+b-c
- D.3（a+b-c）
C
分析：只要运用求平均数公式：
即可求出．
解答：∵x1、x2、x3的平均数
（x1+x2+x3）=a，y1、y2、y3的平均数（y1+y2+y3）=b，z1、z2、z3的平均数（z1+z2+z3）=c
∴x1+y1-z1+x2+y2-z2+x3+y3-z3的平均数
=（x1+y1-z1+x2+y2-z2+x3+y3-z3）
=[（x1+x2+x3）+（y1+y2+y3）-（z1+z2+z3）]
=（x1+x2+x3）+（y1+y2+y3）-（z1+z2+z3）
=a+b-c．
故选C．
点评：本题考查的是样本平均数的求法．熟记公式是解决本题的关键．
分析：只要运用求平均数公式：
即可求出．解答：∵x1、x2、x3的平均数
（x1+x2+x3）=a，y1、y2、y3的平均数（y1+y2+y3）=b，z1、z2、z3的平均数（z1+z2+z3）=c∴x1+y1-z1+x2+y2-z2+x3+y3-z3的平均数
=
（x1+y1-z1+x2+y2-z2+x3+y3-z3）=
[（x1+x2+x3）+（y1+y2+y3）-（z1+z2+z3）]=
（x1+x2+x3）+（y1+y2+y3）-（z1+z2+z3）=a+b-c．
故选C．
点评：本题考查的是样本平均数的求法．熟记公式是解决本题的关键．
练习册系列答案
学习实践园地系列答案
相关题目
B．
C．
D．