题目内容
【题目】在等边三角形![]() 中,点
中,点![]() 从点
从点![]() 出发沿射线
出发沿射线![]() 运动,同时点
运动,同时点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 的延长线运动,
的延长线运动,![]() 、
、![]() 两点运动的速度相同,
两点运动的速度相同,![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.

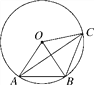
(1)如图①,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
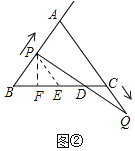
(2)如图②,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() .
.
①当点![]() 在线段
在线段![]() 上运动时,求证:
上运动时,求证:![]() .
.
②当点![]() 在线段
在线段![]() 延长线上运动时,直接写出
延长线上运动时,直接写出![]() 、
、![]() 与
与![]() 之间的数量关系.
之间的数量关系.
【答案】(1)证明见解析;(2)①证明见解析;②![]() .
.
【解析】
(1)根据![]() 易得△BPE 为等边三角形,所以BP=PE,再由速度相同可得BP=CQ,所以EP=CQ;
易得△BPE 为等边三角形,所以BP=PE,再由速度相同可得BP=CQ,所以EP=CQ;
(2)①过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,可证明
,可证明![]() ,可得ED=CD,在等边三角形BPE中,由三线合一可知,F为BE中点,然后可得出
,可得ED=CD,在等边三角形BPE中,由三线合一可知,F为BE中点,然后可得出![]() ;
;
②作PG∥AC交BC的延长线于G,
同理可证明:△PGD≌△QCD,BF=FG
(1)∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() 是等边三角形.∴
是等边三角形.∴![]() .
.
∵![]() 、
、![]() 两点运动的速度相同,且同时出发,
两点运动的速度相同,且同时出发,
∴![]() .∴
.∴![]() .
.
(2)①过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,![]() .
.
由(1)得![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 是等边三角形,
是等边三角形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
② ![]() . 理由如下:
. 理由如下:
作PG∥AC交BC的延长线于G,
同理可证明:△PGD≌△QCD,BF=FG
∴DC=DG
∴BG-CG=BC,
∴2BF-2CD=BC
即![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
【题目】将图1中的正方形剪开得到图2,则图2中共有4个正方形;将图2中的一个正方形剪开得到图3,图3中共有7个正方形;将图3中4个较小的正方形中的一个剪开得到图4,则图4中共有10个正方形,照这个规律剪下去:

(1)根据图中的规律补全表:
图形标号 | 1 | 2 | 3 | 4 | 5 | 6 |
正方形个数 | 1 | 4 | 7 | 10 | _____ | _____ |
(2)第n个图形中有多少个正方形?
(3)当n=673时,图形中有多少个正方形?