题目内容
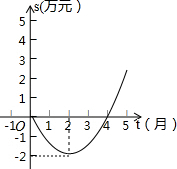 (2013•金平区模拟)如图的二次函数图象(部分)刻画了某公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
(2013•金平区模拟)如图的二次函数图象(部分)刻画了某公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:(1)写出二次函数对称轴与顶点坐标;
(2)求累积利润s(万元)与时间t(月)之间的函数关系式.
分析:(1)由函数的图象可直接写出二次函数对称轴与顶点坐标;
(2)根据(1)可知抛物线的顶点坐标为(2,-2)所以可设设二次函数的解析式为s=a(t-2)2-2,由图可知当t=0,s=0,所以求出a的值,进而求出累积利润s(万元)与时间t(月)之间的函数关系式.
(2)根据(1)可知抛物线的顶点坐标为(2,-2)所以可设设二次函数的解析式为s=a(t-2)2-2,由图可知当t=0,s=0,所以求出a的值,进而求出累积利润s(万元)与时间t(月)之间的函数关系式.
解答:解:(1)由二次函数的图象可知:对称轴为t=2,顶点坐标为(2,-2);
(2)解法一:∵二次函数的顶点坐标为(2,-2),
∴设二次函数的解析式为s=a(t-2)2-2,
由图可知当t=0,s=0,∴0=a(0-2)2-2,
∴a=
,(6分)
∴s=
(t-2)2-2,即s=
t2-2t.
解法二:
∵二次函数过原点,
∴设二次函数的解析式为s=at2+bt,
由图可知当t=4,时s=0;当t=2,时s=-2.
∴
,
∴
∴二次函数的解析式为s=
t2-2t.
(2)解法一:∵二次函数的顶点坐标为(2,-2),
∴设二次函数的解析式为s=a(t-2)2-2,
由图可知当t=0,s=0,∴0=a(0-2)2-2,
∴a=
| 1 |
| 2 |
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
解法二:
∵二次函数过原点,
∴设二次函数的解析式为s=at2+bt,
由图可知当t=4,时s=0;当t=2,时s=-2.
∴
|
∴
|
∴二次函数的解析式为s=
| 1 |
| 2 |
点评:本题考查了由函数图象会确定抛物线的顶点坐标和对称轴以及用顶点式或一般式求二次函数的解析式,是中考常见题型,

练习册系列答案
相关题目
 (2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( )
(2013•金平区模拟)木工师傅在做完门框后,为防止变形常常像图中所示那样钉上两条斜拉的木板条(即图中的AB和CD),这样做的根据是( ) (2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是
(2013•金平区模拟)一个自然数的立方,可以分裂成若干个连续奇数的和.例如:23,33和43分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即23=3+5;33=7+9+11;43=13+15+17+19;…;若73也按照此规律来进行“分裂”,则73“分裂”出的奇数中,最大的奇数是