题目内容
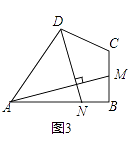
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC= ![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
【答案】
(1)证明:如图1
 ,
,
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)解:cos∠ABC= ![]() ,AB=12,得
,AB=12,得
OB=8.
由勾股定理,得
AO= ![]() =4
=4 ![]() .
.
由三角形的面积,得
S△AOB= ![]() ABOE=
ABOE= ![]() OBAO,
OBAO,
OE= ![]() =
= ![]() ,
,
半圆O所在圆的半径是 ![]()
【解析】本题考查了切线的判定与性质,利用切线的判定是解题关键,利用面积相等得出关于OE的长是解题关键.(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据余弦,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.

练习册系列答案
相关题目