题目内容
已知四边形ABCD的对角线AC、BD相交于点O,下列条件中能够判断有一组对边平行的是
- A.AD:BC=AO:CO
- B.AD:BC=DO:CO
- C.AO:BO=CO:DO
- D.AO:BO=DO:CO
C
分析:相似三角形的判定定理之一是:两边对应成比例,且夹角相等的两个三角形相似,先根据选项证两三角形相似,得出对应角相等,再看看是否符合平行线的判定定理即可.
解答:
解:相似三角形的判定定理之一是:两边对应成比例,且夹角相等的两个三角形相似,
A、根据AD:BC=AO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
B、根据AD:BC=DO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
C、∵AO:OB=CO:DO,
∴ =
= ,
,
∵∠AOB=∠COD,
∴△AOB∽△COD,
∴∠BAC=∠DCA,
∴AB∥CD,故本选项正确;
D、∵AO:BO=DO:CO,∠AOD=∠COB,
∴△AOD∽△BOC,
∴∠DAO=∠CBO,∠ADO=∠BCO,
∴不能推出AD∥BC或AB∥CD,故本选项错误;
故选C.
点评:本题考查了相似三角形的性质和判定,平行线的判定等知识点,注意:两边对应成比例,且夹角相等的两个三角形相似,内错角相等,两直线平行.相似三角形的对应角相等.
分析:相似三角形的判定定理之一是:两边对应成比例,且夹角相等的两个三角形相似,先根据选项证两三角形相似,得出对应角相等,再看看是否符合平行线的判定定理即可.
解答:

解:相似三角形的判定定理之一是:两边对应成比例,且夹角相等的两个三角形相似,
A、根据AD:BC=AO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
B、根据AD:BC=DO:CO,不具备夹角相等,即不能推出两三角形相似,即不能得逞两内错角相等,根据平行线的判定不能推出两边平行,故本选项错误;
C、∵AO:OB=CO:DO,
∴
 =
= ,
,∵∠AOB=∠COD,
∴△AOB∽△COD,
∴∠BAC=∠DCA,
∴AB∥CD,故本选项正确;
D、∵AO:BO=DO:CO,∠AOD=∠COB,
∴△AOD∽△BOC,
∴∠DAO=∠CBO,∠ADO=∠BCO,
∴不能推出AD∥BC或AB∥CD,故本选项错误;
故选C.
点评:本题考查了相似三角形的性质和判定,平行线的判定等知识点,注意:两边对应成比例,且夹角相等的两个三角形相似,内错角相等,两直线平行.相似三角形的对应角相等.

练习册系列答案
相关题目
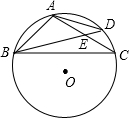 如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=
如图,已知四边形ABCD的外接圆⊙O的半径为2,对角线AC与BD的交点为E,AE=EC,AB=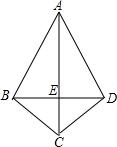 如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为
如图,△ABC与△ADC关于直线AC对称,连接BD,若已知四边形ABCD的面积是125,AC=25,则BD的长为 如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( )
如图,已知四边形ABCD的对角线互相垂直,若适当添加一个条件,就能判定该四边形是菱形.那么这个条件可以是( ) 如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )
如图,已知四边形ABCD的四个顶点的坐标分别为A(0,0),B(9,0),C(7,5),D(2,7),将该四边形各顶点的横坐标都增加2,纵坐标都增加3,其面积为( )