题目内容
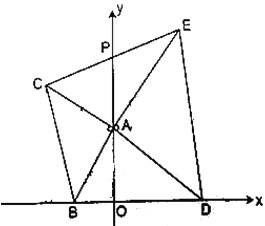
【题目】平面直角坐标系![]() 中,
中,![]() ,
,![]() 分别在
分别在![]() 轴正半轴和
轴正半轴和![]() 轴负半轴上,
轴负半轴上,![]() 在第二象限,满足:
在第二象限,满足:![]() ,
,![]() .已知
.已知![]() .
.
(1)求![]() ,
,![]() 的坐标;
的坐标;
(2)求点![]() 的坐标及
的坐标及![]() 的面积;
的面积;
(3)已知![]() 是
是![]() 轴的正半轴上一点,
轴的正半轴上一点,![]() ,
,![]() 在第一象限,
在第一象限,![]() ,
,![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() .
.
①求证:![]() .
.
②在点![]() 的移动过程中,给出以下两个结论:(i)
的移动过程中,给出以下两个结论:(i)![]() 的值不变;(ii)
的值不变;(ii)![]() 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
【答案】(1)A(0,4),B(-2,0);
(2)C(-4,6);10.
(3)①见详解;②![]() 的值不变,等于
的值不变,等于![]() .
.
【解析】
(1)根据非负数的性质,即可求出结果;
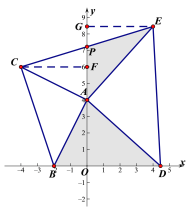
(2)如图,过点C作CF⊥y轴于F,先证△ACF≌△BAO,从而得到CF=OA,AF=OB,又因为点C在第四象限,故可得点C的坐标,根据勾股定理求得AC=AB=2![]() ,再根三角形的面积计算公式即可求得△ABC的面积;
,再根三角形的面积计算公式即可求得△ABC的面积;
(3)①过点E作EG⊥y轴于点G,先证△AGE≌△DOA,得到GE=OA=4,故GE=CF,再根据AAS证得△GPE≌△FOC,从而得到PC=PE;②利用面积法进行等量代换即可得到![]() =
=![]() .
.
解:(1)∵![]() ,
,
∴![]() ,解得:
,解得:![]() .
.
∴A(0,4),B(-2,0).
(2)过点C作CF⊥y轴于F,
∴∠CFA=∠AOB=90°,
∴∠CAF+∠ACF=90°.
∵![]() ,
,
∴∠CAF+∠BAO=90°.
∴∠ACF=∠BAO
在△ACF和△BAO中
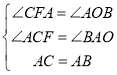
∴△ACF≌△BAO.
∴CF=OA=4,AF=OB=2
∵点C在第二象限,
∴C(-4,6).
在Rt△ABO中,
AB=![]() =
=![]() =2
=2![]() .
.
∵∠BAC=90°,AC=AB=2![]() .
.
∴![]() =
=![]() AC=
AC=![]() =10.
=10.
(3)①过点E作EG⊥y轴于G,
∵∠EAD=90°,
∴∠DAO+∠GAE=90°.
∵∠AEG+∠GAE=90°,
∴∠DAO=∠AEG.
在△AOD和△EGA中
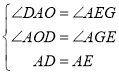
∴△AOD≌△EGA.
∴GE=OA=4.
∵CF=OA,
∴CF=GE.
∵CF⊥y轴,EG⊥y轴,
∴∠PGE=∠PFC=90°.
在△FPC和△GPE中
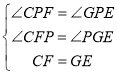
∴△FPC≌△GPE.
∴PC=PE.
②![]() 的值不变,理由如下:
的值不变,理由如下:
∵PC=PE,
∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]()
∵△ACF≌△BAO,
∴![]() =
=![]() .
.
∵△AOD≌△EGA.
∴![]() =
=![]()
∵![]() =
=![]() +
+![]()
∴![]() =
=![]() +
+![]()
∵![]() =
=![]() +
+![]()
∴![]() =
=![]() +
+![]() +
+![]()
=![]() +
+![]() +
+![]()
=![]() .
.
∴![]() =
=![]() =
=![]() .
.

 特高级教师点拨系列答案
特高级教师点拨系列答案