题目内容
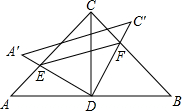（2010•资阳）如图，已知△ABC是等腰直角三角形，CD是斜边AB的中线，△ADC绕点D旋转一定角度得到△A'DC'，A'D交AC于点E，DC'交BC于点F，连接EF，若| A′E |
| ED |
| 2 |
| 5 |
| EF |
| A′C′ |
| 5 |
| 7 |
| 5 |
| 7 |
分析：根据等腰直角三角形的性质及旋转的性质，运用“ASA”证明△ADE≌△CDF，得DE=DF．则有DE：DA′=DF：DC′，得EF∥A′C′．根据相似三角形性质求解．
解答：解：∵△ABC是等腰直角三角形，CD是斜边AB的中线，
∴CD⊥AB，CD=AD，∠A=∠BCD=45°．
又∵∠ADE=90°-∠CDE=∠CDF，
∴△ADE≌△CDF （ASA）
∴DE=DF．
∵DA=DA′，DC=DC′，
∴DE：DA′=DF：DC′，
∴EF∥A′C′．
∴△DEF∽△DA′C′，
∴
=
．
∵
=
，则
=
，
∴
=
．
故答案为
．
∴CD⊥AB，CD=AD，∠A=∠BCD=45°．
又∵∠ADE=90°-∠CDE=∠CDF，
∴△ADE≌△CDF （ASA）
∴DE=DF．
∵DA=DA′，DC=DC′，
∴DE：DA′=DF：DC′，
∴EF∥A′C′．
∴△DEF∽△DA′C′，
∴
| EF |
| A′C′ |
| DE |
| DA′ |
∵
| A′E |
| ED |
| 2 |
| 5 |
| DE |
| DA′ |
| 5 |
| 7 |
∴
| EF |
| A′C′ |
| 5 |
| 7 |
故答案为
| 5 |
| 7 |
点评：此题考查等腰三角形性质、旋转的性质、全等三角形的判定与性质及平行线的判定和性质等知识点，综合性较强．
练习册系列答案
相关题目
（2010•资阳）如图，已知直线l：y=kx+b与双曲线C：
（2010•资阳）如图，A为⊙O上一点，从A处射出的光线经圆周4次反射后到达F处．如果反射前后光线与半径的夹角均为50°，那么∠AOE的度数是（ ）
（2010•资阳）如图，在直角梯形ABCD中，已知AD∥BC，AB=3，AD=1，BC=6，∠A=∠B=90°．设动点P、Q、R在梯形的边上，始终构成以P为直角顶点的等腰直角三角形，且△PQR的一边与梯形ABCD的两底平行．
（2010•资阳）如图，已知A、B、C是数轴上异于原点O的三个点，且O为AB的中点，B为AC的中点．若点B对应的数是x，点C对应的数是x2-3x，求x的值．
（2010•资阳）如图，已知直线y=2x+2交y轴于点A，交x轴于点B，直线l：y=-3x+9