题目内容
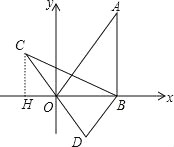
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( ).
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD.若点B的坐标为(2,0),则点C的坐标为( ).

A.(﹣1,![]() ) B.(﹣2,
) B.(﹣2,![]() )
)
C.(﹣![]() ,1) D.(﹣
,1) D.(﹣![]() ,2)
,2)
【答案】A.
【解析】
试题分析:作CH⊥x轴于H,如图,
先根据一次函数图象上点的坐标特征确定A(2,2![]() ),再利用旋转的性质得BC=BA=2
),再利用旋转的性质得BC=BA=2![]() ,∠ABC=60°,则∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三边的关系可计算出CH=
,∠ABC=60°,则∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三边的关系可计算出CH=![]() BC=
BC=![]() ,BH=
,BH=![]() CH=3,所以OH=BH﹣OB=3﹣2=1,于是可写出C点坐标.先作CH⊥x轴于H,如图,∵点B的坐标为(2,0),AB⊥x轴于点B,∴A点横坐标为2,当x=2时,y=
CH=3,所以OH=BH﹣OB=3﹣2=1,于是可写出C点坐标.先作CH⊥x轴于H,如图,∵点B的坐标为(2,0),AB⊥x轴于点B,∴A点横坐标为2,当x=2时,y=![]() x=2
x=2![]() ,∴A(2,2
,∴A(2,2![]() ),∵△ABO绕点B逆时针旋转60°得到△CBD,∴BC=BA=2
),∵△ABO绕点B逆时针旋转60°得到△CBD,∴BC=BA=2![]() ,∠ABC=60°,∴∠CBH=30°,在Rt△CBH中,CH=
,∠ABC=60°,∴∠CBH=30°,在Rt△CBH中,CH=![]() BC=
BC=![]() ,BH=
,BH=![]() CH=3,OH=BH﹣OB=3﹣2=1,∴C(﹣1,
CH=3,OH=BH﹣OB=3﹣2=1,∴C(﹣1,![]() ).故选:A.
).故选:A.

练习册系列答案
相关题目