题目内容
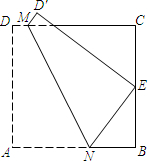（2013•大庆模拟）如图，在正方形纸片ABCD中，E为BC的中点．将纸片折叠，使点A与点E重合，点D落在点D′处，MN为折痕．若梯形ADMN的面积为S1，梯形BCMN的面积为S2，则| S1 |
| S2 |
| 3 |
| 5 |
| 3 |
| 5 |
分析：因为两个梯形的高相等，所以面积比即为边长（DM+AN）与（BN+CM）的比，所以求出DM与BN之间的关系即可．
解答：解：连接MA，ME，
由翻折可得，AN=NE，AM=ME，
设AB=2x，AN=a，在Rt△BEN中，a2=（2x-a）2+x2，
解得：a=
x，
在Rt△ADM，设DM=b，则AM2=（2x）2+b2，
在Rt△EMC中，CM=2x-b，（2x-b）2+x2=（2x）2+b2，
则DM=b=
x，
∴
=
=
=
．
故答案为：
．
由翻折可得，AN=NE，AM=ME，
设AB=2x，AN=a，在Rt△BEN中，a2=（2x-a）2+x2，
解得：a=
| 5 |
| 4 |
在Rt△ADM，设DM=b，则AM2=（2x）2+b2，
在Rt△EMC中，CM=2x-b，（2x-b）2+x2=（2x）2+b2，
则DM=b=
| 1 |
| 4 |
∴
| S1 |
| S2 |
| DM+AN |
| BN+CM |
| ||||
|
| 3 |
| 5 |
故答案为：
| 3 |
| 5 |
点评：本题考查了翻折变换的知识，要求同学们理解轴对称图形的性质及正方形的性质，能够利用其性质求解一些简单的问题．
练习册系列答案
相关题目
（2013•大庆模拟）已知正五边形的对称轴是过任意一个顶点与该顶点对边中点的直线．如图所示的正五边形中相邻两条对称轴所夹锐角α的度数为（ ）