题目内容
 如图,PA、PB分别是⊙O的切线,切点分别为A、B两点,若∠P=40°,则弦AB所对圆周角的度数是
如图,PA、PB分别是⊙O的切线,切点分别为A、B两点,若∠P=40°,则弦AB所对圆周角的度数是分析:由PA、PB是⊙O的切线,∠P=40°,根据切线的性质,易求得∠AOB的度数,然后又圆周角定理,可求得当点C在优弧AB上时,∠ACB的值,由圆的内接四边形的性质,可求得当点C′在劣弧AB上时,∠AC′B的度数,继而求得答案.
解答:解:理解OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠P=40°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=140°,
∴当点C在优弧AB上时,∠ACB=
∠AOB=70°;
当点C′在劣弧AB上时,∠AC′B=180°-∠ACB=110°.
∴弦BA所对的圆周角的度数是:70°或110°.
故答案为:70°或110°

∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠P=40°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=140°,
∴当点C在优弧AB上时,∠ACB=
| 1 |
| 2 |
当点C′在劣弧AB上时,∠AC′B=180°-∠ACB=110°.
∴弦BA所对的圆周角的度数是:70°或110°.
故答案为:70°或110°
点评:此题考查了切线的性质、圆周角定理以及圆的内接四边形的性质.此题难度不大,注意掌握弦所对的圆周角有两种且互补.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
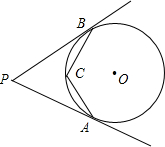 如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB=
如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,已知∠P=50°,则∠ACB= 7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( )
7、如图,PA、PB分别切圆O于A、B两点,C为劣弧AB上一点,∠APB=30°,则∠ACB=( ) 7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是
7、如图,PA,PB分别切⊙O于点A,B,点C是AB上一点,过C作⊙O的切线,交PA,PB于点D,E,若PA=6cm,则△PDE的周长是 (2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°.
(2012•绵阳)如图,PA、PB分别切⊙O于A、B,连接PO、AB相交于D,C是⊙O上一点,∠C=60°. 如图,PA,PB分别切⊙O于点A和点B,C是
如图,PA,PB分别切⊙O于点A和点B,C是