题目内容
抛物线y=x2-4x+c的顶点在x轴上，则c的值是（ ）A．0
B．4
C．-4
D．2
【答案】分析：根据二次函数y=ax2+bx+c的顶点坐标公式及点在x轴上的纵坐标为0的特征作答．
解答：解：根据二次函数y=ax2+bx+c的顶点坐标为（-
，
）
∵抛物线y=x2-4x+c的顶点在x轴上，即y=0
∴
=0
∴c=4．
故选B．
点评：此题考查了二次函数的顶点坐标，解题的关键是找准对应的各系数．
解答：解：根据二次函数y=ax2+bx+c的顶点坐标为（-
，）∵抛物线y=x2-4x+c的顶点在x轴上，即y=0
∴
=0∴c=4．
故选B．
点评：此题考查了二次函数的顶点坐标，解题的关键是找准对应的各系数．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
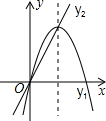如图，抛物线y1=-x2+4x和直线y2=2x．当y1＞y2时，x的取值范围是（ ）| A、0＜x＜2 | B、x＜0或x＞2 | C、x＜0或x＞4 | D、0＜x＜4 |