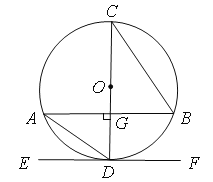
题目内容
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上的动点(含端点
上的动点(含端点![]() ,
,![]() ),连结
),连结![]() ,以
,以![]() 所在直线为对称轴作点
所在直线为对称轴作点![]() 的对称点
的对称点![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() ,
,![]() 的中点,连结
的中点,连结![]() ,
,![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的长;
的长;
(3)以![]() 其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
其中两边为邻边构造平行四边形,当所构造的平行四边形恰好是菱形时,这时该菱形的面积是________.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先利用三角形中位线定理得到![]() ,故
,故![]() ,可得四边形
,可得四边形![]() 为平行四边形,再根据对称性得到
为平行四边形,再根据对称性得到![]() ,即可得到
,即可得到![]() ,即邻边相等的平行四边形是菱形,故可求解;
,即邻边相等的平行四边形是菱形,故可求解;
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,根据菱形的面积可求出
,根据菱形的面积可求出![]() ,再根据中位线及正方形的性质分别求出PN,PQ,CN,AQ,设
,再根据中位线及正方形的性质分别求出PN,PQ,CN,AQ,设![]() ,在
,在![]() 中,
中,![]() 得到方程求出x即可求解;
得到方程求出x即可求解;
(3)过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,分当
,分当![]() 时、当
时、当![]() 时、当
时、当![]() 时分别求出菱形的面积即可.
时分别求出菱形的面积即可.
解:(1)∵![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∴四边形![]() 为平行四边形.
为平行四边形.
∵![]() 与
与![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为菱形.
为菱形.
(2)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,如图.
,如图.
![]() 四边形
四边形![]()
![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
设![]() ,
,
∴![]() .在
.在![]() 中,
中,![]() ,即
,即![]() ,
,
解得![]() ,
,
∴![]() .
.

(3)菱形的面积为![]() 或
或![]() 或
或![]() .理由如下:
.理由如下:
如图,过点![]() 作
作![]() 的垂线,分别交
的垂线,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .
.
当![]() 时,点
时,点![]() 在点
在点![]() 处,
处,
此时![]() 菱形
菱形![]() ;
;
当![]() 时,此时
时,此时![]() 是正三角形,
是正三角形,
∴![]() ,PK=
,PK=![]() BP=5cm,
BP=5cm,
![]() 菱形
菱形![]() ;
;
当![]() 时,此时
时,此时![]() 是正三角形,
是正三角形,![]()
∴![]()
则CL=![]() CP=5cm,
CP=5cm,
∴![]() ,
,![]() ,
,
![]() 菱形
菱形![]() .
.
综上所述,菱形的面积为![]() 或
或![]() 或
或![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】研究问题:一个不透明的盒中装有若干个白球,怎样估算白球的数量?
操作方法:先从盒中摸出8个球,画上记号放回盒中,再进行摸球实验.摸球实验的要求:先搅拌均匀,每次摸出一个球,放回盒中,再继续.
统计结果如表:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到有记号球的次数m | 25 | 44 | 57 | 105 | 160 | 199 |
摸到有记号球的频率 | 0.25 | 0.22 | 0.19 | 0.21 | 0.20 | 0.20 |
(1)请你完成上表中数据,并估计摸到有记号球的概率是多少?
(2)估计盒中共有球多少个?没有记号球有多少个?