题目内容
20.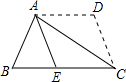 如图,等腰梯形ABCD中,AD∥BC,AB=CD,将梯形ABCD沿对角线AC折叠,使D点落在BC边的点E处,若BE=2,CE=3,则折叠线AC的长度为( )
如图,等腰梯形ABCD中,AD∥BC,AB=CD,将梯形ABCD沿对角线AC折叠,使D点落在BC边的点E处,若BE=2,CE=3,则折叠线AC的长度为( )| A. | 5 | B. | $3\sqrt{2}$ | C. | $2\sqrt{6}$ | D. | 2$\sqrt{5}$ |
分析 作AF⊥BC于点F,根据等腰梯形的性质及折叠的性质得到AE=EC=CD=AB=3,然后利用勾股定理求得AF和ACD的长即可.
解答  解:作AF⊥BC于点F,
解:作AF⊥BC于点F,
∵AD∥BC,
∴∠DAC=∠BCA,
∵使D点落在BC边的点E处,
∴∠DAC=∠EAC,
∴∠EAC=∠ACE,
∴AE=EC=CD=AB=3,
∴FB=FE=1,
∴AF2=AF2-BF2=9-1=8,
∴AC=$\sqrt{A{F}^{2}+F{C}^{2}}$=$\sqrt{8+16}$=2$\sqrt{6}$,
故选C.
点评 本题考查了等腰梯形的性质及折叠的性质,解题的关键是了解折叠前后对应相等的量,难度不大.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
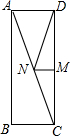 如图,在矩形ABCD中,AD=3,AB=9,M是DC上一点,DM=4,N是AC上的一个动点,则△DMN的周长的最小值是$\sqrt{34}$+4.
如图,在矩形ABCD中,AD=3,AB=9,M是DC上一点,DM=4,N是AC上的一个动点,则△DMN的周长的最小值是$\sqrt{34}$+4. 如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,求旗杆的高度?
如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,求旗杆的高度?