Question

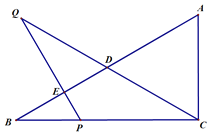
【题目】已知,如图, 在中, ,,,P是边BC上的一动点，过点P作PE⊥AB,垂足为E，延长PE至点Q，使PQ=PC, 联结交边AB于点.

（1）求AD的长；

（2）设,的面积为y, 求y关于x的函数解析式，并写出定义域；

（3）过点C作, 垂足为F, 联结PF、QF, 试探索当点P在边BC的什么位置时，为等边三角形？请指出点P的位置并加以证明.

Answer 1

【答案】（1）证明见解析；（2），定义域为．（3）点是边的中点，证明见解析.

【解析】

（1）根据直角三角形的性质和三角形的内角和定理，进行计算，即可得到答案；

（2）作，垂足为点．根据勾股定理进行计算，即可得到答案；

（3）根据等腰三角形的性质和判定即可得到答案.

解：（1）在中，，，∴

∵ ∴．

∵ ∴90° ∴90°．

∵=90°，∴

∵，∴，∴

（2）作，垂足为点．

∵90°，∴=90°，∴，∴

∴，∴

∴，即

定义域为．

(3)点是边的中点.

证明：∵,点是边的中点.

∴

∵，

∴

∴是等边三角形

∴

∵

∴

∵,

∴

∴是等边三角形