题目内容
已知m、n互为相反数,且mn≠0,a、b互为负倒数,|x-2|=4,求x3-(1+m+n-ab)x2+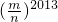 的值.
的值.
解:∵m、n互为相反数,且mn≠0,a、b互为负倒数,
∴m+n=0, =-1,ab=-1,
=-1,ab=-1,
∵|x-2|=4,
∴x=6或x=-2,
∴x3-(1+m+n-ab)x2+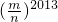 =x3-(1+0+1)x2+(-1)2013=x3-2x2-1,
=x3-(1+0+1)x2+(-1)2013=x3-2x2-1,
∴当x=6时,原式=63-2×62-1=143;
当x=-2时,原式=(-2)3-2×(-2)2-1=-1;
分析:根据m、n互为相反数,且mn≠0,a、b互为负倒数,得出m+n=0, =-1,ab=-1,再根据|x-2|=4,求出x的值,最后把要求的式子进行整理,把x的值分别代入即可得出答案.
=-1,ab=-1,再根据|x-2|=4,求出x的值,最后把要求的式子进行整理,把x的值分别代入即可得出答案.
点评:此题考查了有理数的混合运算,用到的知识点是相反数、绝对值、倒数,解题的关键是根据相反数、绝对值、倒数的定义分别求出m+n=0, =-1,ab=-1,x=6或x=-2.
=-1,ab=-1,x=6或x=-2.
∴m+n=0,
 =-1,ab=-1,
=-1,ab=-1,∵|x-2|=4,
∴x=6或x=-2,
∴x3-(1+m+n-ab)x2+
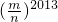 =x3-(1+0+1)x2+(-1)2013=x3-2x2-1,
=x3-(1+0+1)x2+(-1)2013=x3-2x2-1,∴当x=6时,原式=63-2×62-1=143;
当x=-2时,原式=(-2)3-2×(-2)2-1=-1;
分析:根据m、n互为相反数,且mn≠0,a、b互为负倒数,得出m+n=0,
 =-1,ab=-1,再根据|x-2|=4,求出x的值,最后把要求的式子进行整理,把x的值分别代入即可得出答案.
=-1,ab=-1,再根据|x-2|=4,求出x的值,最后把要求的式子进行整理,把x的值分别代入即可得出答案.点评:此题考查了有理数的混合运算,用到的知识点是相反数、绝对值、倒数,解题的关键是根据相反数、绝对值、倒数的定义分别求出m+n=0,
 =-1,ab=-1,x=6或x=-2.
=-1,ab=-1,x=6或x=-2. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目