题目内容
 如图,边长为20的正方形ABCD截去一角成为五边形ABCEF,其中DE=10,DF=5,若点P在线段EF上使矩形PMBN有最大面积时,则PE的长度为________.
如图,边长为20的正方形ABCD截去一角成为五边形ABCEF,其中DE=10,DF=5,若点P在线段EF上使矩形PMBN有最大面积时,则PE的长度为________.
5
分析:延长NP交ED于G点,设PG=x,先由PG∥DF,得出△EPG∽△EFD,根据相似三角形的性质得出EG=2x,MP=10+2x,进而得到S矩形PNBM是x的二次函数,再根据二次函数的性质得出矩形PMBN有最大面积时PG的值,从而求出此时PE的长度.
解答: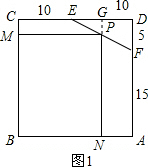 解:如图1,延长NP交ED于G点,
解:如图1,延长NP交ED于G点,
设PG=x,则PN=20-x,
∵PG∥DF,
∴△EPG∽△EFD,
∴PG:DF=EG:ED,
即EG:10=x:5,
∴EG=2x,
 ∴MP=CG=CE+EG=10+2x,
∴MP=CG=CE+EG=10+2x,
∴S矩形PNBM=PM•PN=(10+2x)(20-x)=-2x2+30x+200=-2(x- )2+
)2+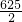 (0≤x≤5),
(0≤x≤5),
∵-2<0,PG=x≤DF=5,
∴当x=5时,S矩形PNBM有最大值300.
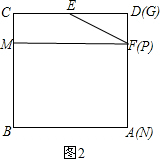
当PG=5时,如图2,此时P与F重合.
在△PDE中,∠PDE=90°,PD=5,DE=10,
由勾股定理,得PE=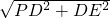 =5
=5 .
.
故答案为5 .
.
点评:本题考查了正方形的性质,相似三角形的判定与性质,二次函数最值的求法,综合性较强,有一定难度.本题根据相似三角形的性质得出EG=2x,进而得到S矩形PNBM是x的二次函数是解题的关键.

分析:延长NP交ED于G点,设PG=x,先由PG∥DF,得出△EPG∽△EFD,根据相似三角形的性质得出EG=2x,MP=10+2x,进而得到S矩形PNBM是x的二次函数,再根据二次函数的性质得出矩形PMBN有最大面积时PG的值,从而求出此时PE的长度.
解答:
 解:如图1,延长NP交ED于G点,
解:如图1,延长NP交ED于G点,设PG=x,则PN=20-x,
∵PG∥DF,
∴△EPG∽△EFD,
∴PG:DF=EG:ED,
即EG:10=x:5,
∴EG=2x,
 ∴MP=CG=CE+EG=10+2x,
∴MP=CG=CE+EG=10+2x,∴S矩形PNBM=PM•PN=(10+2x)(20-x)=-2x2+30x+200=-2(x-
 )2+
)2+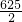 (0≤x≤5),
(0≤x≤5),∵-2<0,PG=x≤DF=5,
∴当x=5时,S矩形PNBM有最大值300.
当PG=5时,如图2,此时P与F重合.
在△PDE中,∠PDE=90°,PD=5,DE=10,
由勾股定理,得PE=
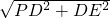 =5
=5 .
.故答案为5
 .
.点评:本题考查了正方形的性质,相似三角形的判定与性质,二次函数最值的求法,综合性较强,有一定难度.本题根据相似三角形的性质得出EG=2x,进而得到S矩形PNBM是x的二次函数是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 12、如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用
12、如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用

 如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用________块.
如图所示,在大房间的一面墙壁上,边长为15cm的正六边形A(如图(1))横排20块和以其一部分所形成的梯形B,三角形C,D,E,菱形F等六种瓷砖毫无空隙地排列在一起,已知墙壁高3.3m,请你仔细观察各层瓷砖的排列特点,计算其中菱形F瓷砖需使用________块.