题目内容
已知抛物线y=ax2-5ax+4a与x轴交于点A、B(A在B的左边),与y轴交于C点,且过点(5,4).(1)求a的值;
(2)设顶点为P,求△ACP的面积;
(3)在该抛物线上是否存在点Q,使S△ABQ=
| 1 | 2 |
(4)画出该函数的图象,根据图象回答当x为何值时,y≥0?
(5)写出当2≤x≤6时,该函数的最大值和最小值.
分析:(1)把点(5,4)代入y=ax2-5ax+4a解得a;
(2)求出A、P、C点的坐标,过直线PC与x轴的交点M,S△APC=S△AMC+S△AMP;
(3)该抛物线上存在点Q,使S△ABQ=
S△ABP,确定Q点的纵坐标,代入抛物线解析式求出横坐标即可;
(4)由点A、B、C、P四点画出图象,由A、B两点的坐标得出x的取值范围;
(5)因为x=2,x=6在x=
的右侧,a>0,y随x的增大而增大,把x=2,x=6代入解析式求得函数的最大值和最小值.
(2)求出A、P、C点的坐标,过直线PC与x轴的交点M,S△APC=S△AMC+S△AMP;
(3)该抛物线上存在点Q,使S△ABQ=
| 1 |
| 2 |
(4)由点A、B、C、P四点画出图象,由A、B两点的坐标得出x的取值范围;
(5)因为x=2,x=6在x=
| 5 |
| 2 |
解答:解:(1)把点(5,4)代入y=ax2-5ax+4a
解得a=1;
(2)如图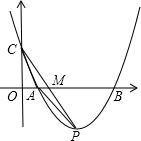 ,
,
由y=x2-5x+4可知,A(1,0),C,0,4),P(
,-
),
过PC的直线为y=-
x+4,与x轴的交点M为(
,0),
S△APC=S△AMC+S△AMP=
×(
-1)×4+
×(
-1)×
=
;
(3)该抛物线上存在点Q.
因为使S△ABQ=
S△ABP,所以点Q的纵坐标的绝对值为
,
当点Q在x轴的上方,由x2-5x+4=
,
解得x=
,
当点Q在x轴的下方,由x2-5x+4=-
,
解得x=
,
由此得出Q点的坐标为:
(
,
),(
,-
)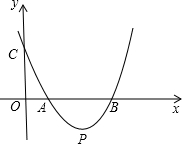
(4)由图象可以看出当x≤1或x≥4时,y≥0.
(5)因为y=x2-5x+4=(x-
)2-
,
所以把x=2,x=6分别代入y=x2-5x+4,
可得当x=2时,y=-2,
当x=6时,y=10,
∴函数的最大值为10,最小值为-
.
解得a=1;
(2)如图
 ,
,由y=x2-5x+4可知,A(1,0),C,0,4),P(
| 5 |
| 2 |
| 9 |
| 4 |
过PC的直线为y=-
| 5 |
| 2 |
| 8 |
| 5 |
S△APC=S△AMC+S△AMP=
| 1 |
| 2 |
| 8 |
| 5 |
| 1 |
| 2 |
| 8 |
| 5 |
| 9 |
| 4 |
| 15 |
| 8 |
(3)该抛物线上存在点Q.
因为使S△ABQ=
| 1 |
| 2 |
| 9 |
| 8 |
当点Q在x轴的上方,由x2-5x+4=
| 9 |
| 8 |
解得x=
10± 3
| ||
| 4 |
当点Q在x轴的下方,由x2-5x+4=-
| 9 |
| 8 |
解得x=
10± 3
| ||
| 4 |
由此得出Q点的坐标为:
(
10±3
| ||
| 4 |
| 9 |
| 8 |
10±3
| ||
| 4 |
| 9 |
| 8 |

(4)由图象可以看出当x≤1或x≥4时,y≥0.
(5)因为y=x2-5x+4=(x-
| 5 |
| 2 |
| 9 |
| 4 |
所以把x=2,x=6分别代入y=x2-5x+4,
可得当x=2时,y=-2,
当x=6时,y=10,
∴函数的最大值为10,最小值为-
| 9 |
| 4 |
点评:本题考查了二次函数解析式的确定、二次函数的对称性、图形面积的求法、方程与函数的关系、分类讨论的思想.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=