题目内容
若an=-
,b2n=2,(n为正整数),求1+(-ab)4n+a3nb6n的值.
| 1 | 3 |
分析:根据an=-
,b2n=2,(n为正整数)可得a4n=
,a3n=-
,b6n=8,b4n=4,然后再代入1+(-ab)4n+a3nb6n中进行计算即可.
| 1 |
| 3 |
| 1 |
| 81 |
| 1 |
| 27 |
解答:解:∵an=-
,b2n=2,(n为正整数),
∴a4n=
,a3n=-
,b6n=8,b4n=4,
∴1+(-ab)4n+a3nb6n
=1+
×4+(-
)×8
=
.
| 1 |
| 3 |
∴a4n=
| 1 |
| 81 |
| 1 |
| 27 |
∴1+(-ab)4n+a3nb6n
=1+
| 1 |
| 81 |
| 1 |
| 27 |
=
| 61 |
| 81 |
点评:此题主要考查了幂的乘方和积的乘方,关键是掌握幂的乘方法则:底数不变,指数相乘;积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 (2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=
(2013•北京)如图,在平面直角坐标系xOy中,已知直线l:y=-x-1,双曲线y=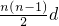 ,求:
,求: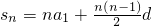 计算:3,5,7,9,11,13,…103这几个数的和.
计算:3,5,7,9,11,13,…103这几个数的和.