题目内容
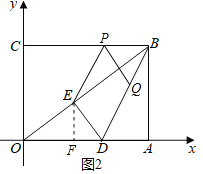
【题目】如图，在平面直角坐标系中，
为坐标原点，矩形
的顶点
，将矩形的一个角沿直线
折叠，使得点
落在对角线
上的点
处，折痕与
轴交于点
.
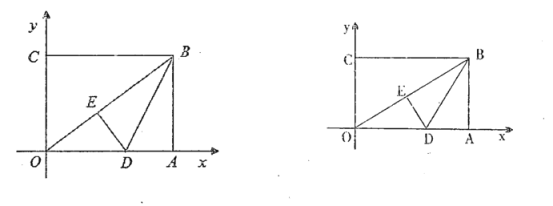
（1）求直线所对应的函数表达式；
（2）若点
在线段上，在线段
上是否存在点
，使以
为顶点的四边形是平行四边形？若存在，请求出点的坐标；若不存在，请说明理由.
【答案】（1）y=2x-10；（2）存在点
，Q（
，
）， 使以
为顶点的四边形为平行四边形.
【解析】
（1）由矩形的性质可得出点B的坐标及OA，AB的长，利用勾股定理可求出OB的长，设AD=a，则DE=a，OD=8-a，OE=OB-BE=10-6=4，利用勾股定理可求出a值，进而可得出点D的坐标，再根据点B，D的坐标，利用待定系数法可求出直线BD所对应的函数表达式；
（2）先假设存在点P 满足条件，过E作
交BC于P作
，交BD 于Q点，这样得到点Q，四边形
即为所求平行四边形，过E作
得
，
可得E点坐标， 根据点B、E坐标求出直线BD的解析式， 又
根据平行的直线，k值相等，求出PE解析式， 再求点出P坐标，从而求解.
（1）由题意，得：点B的坐标为（8，6），OA=8，AB=OC=6，
∴OB= 
=10．
设AD=a，则DE=a，OD=8-a，OE=OB-BE=10-6=4．
∵OD2=OE2+DE2，即（8-a）2=42+a2，
∴a=3，
∴OD=5，
∴点D的坐标为（5，0）．
设直线BD所对应的函数表达式为y=kx+b（k≠0），
将B（8，6），D（5，0）代入y=kx+b，得：
解得：
∴直线BD所对应的函数表达式为y=2x-10．
（2）如图2，假设在线段
上存在点P 使
为顶点的四边形为平行四边形，过E作 交BC于P，过点P作，交BD 于Q点，四边形 即为所求平行四边形，过E作 得 ，，
，
直线
，
又 ，
，
，在线段上存在点P（5，6），
使以为顶点的四边形为平行四边形，
∵
，设点Q的坐标为（m，2m-10），四边形DEPQ为平行四边形，
D（5，0），，点P的纵坐标为6，
∴6-（2m-10）=
-0，解得：m=，
∴点Q的坐标为（，）．
∴存在，点Q的坐标为（，）．
