Question

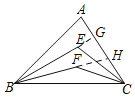
【题目】如图，BE和BF三等分∠ABC，CE和CF三等分∠ACB，∠A＝60°，求∠BEC和∠BFC的度数．

Answer 1

【答案】100°，140°

【解析】

延长BE交AC于G，由三角形外角性质，可得∠BEC＝∠BGC+∠ACE，∠BGC＝∠A+∠ABE，再根据BE和BF三等分∠ABC，CE和CF三等分∠ACB，即可得到∠BEC和∠BFC的度数．

如图，延长BE交AC于G，

由三角形外角性质，可得∠BEC＝∠BGC+∠ACE，∠BGC＝∠A+∠ABE，

∵BE和BF三等分∠ABC，CE和CF三等分∠ACB，

∴∠ABE＝∠ABC，∠ACE＝∠ACB，

又∵∠ABC+∠ACB＝180°﹣∠A，

∴∠BEC＝∠A+∠ABC+∠ACB＝∠A+（180°﹣∠A）＝60°+∠A，

当∠A＝60°时，∠BEC＝60°+×60°＝100°，

同理可得，∠BFC＝∠A+（180°﹣∠A）＝120°+∠A＝120°+×60°＝140°．