题目内容
如图，在△ABC中，∠C＝45°，BC＝10，高AD＝8，矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD交EF于点H．
（1）求证：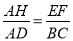 
；
（2）设EF＝x，当x为何值时，矩形EFPQ的面积最大?并求其最大值；
（3）当矩形EFPQ的面积最大时，该矩形EFPQ以每秒1个单位的速度沿射线QC匀速运动(当点Q与点C重合时停止运动)，设运动时间为t秒，矩形EFFQ与△ABC重叠部分的面积为S，求S与t的函数关系式．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
的解集为__________.2016年某中学举行的春季田径径运动会上，参加男子跳高的15名运动员的成绩如表所示：
这些运动员跳高成绩的中位数和众数分别是（ ）
成绩（ | 1.80 | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 |
人数 | 1 | 2 | 4 | 3 | 3 | 2 |
）A. 1.70
，1.65
B. 1.70
，1.70
C. 1.65
，1.60
D. 3
，4
，则AD的长为( )
C. 
D. 1
： 
，过点A(0，1)作y轴的垂线交直线
于点B，过点B作直线
的垂线交y轴于点
；过点
作y轴的垂线交直线
于点
，过点
作直线
的垂线y轴于点A2；……按此作法继续下去，则点A4的坐标为( )