题目内容
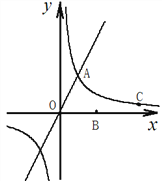
【题目】如图,直线y=kx+b(k≠0)与两坐标轴分别交于点B,C,点A的坐标为(-2,0)点D的坐标为(1,0)
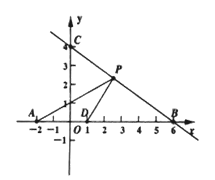
(1)试确定直线BC的函数关系式.
(2)若p(x,y)是直线BC在第一象限内的一个动点,试写出△ADP的面积S与x的函数关系式.
(3)当P运动到什么位置时,△ADP的面积为3?请写出此时点P的坐标,并说明理由.
【答案】(1)y=-![]() x+4;(2) S=-x+6;(3) (3,2)
x+4;(2) S=-x+6;(3) (3,2)
【解析】(1)运用待定系数法即可求出解析式;
(2)利用三角形面积公式即可建立函数关系式;
(3)利用(2)中的函数关系式即可得出答案.
解:(1)设直线BC的函数关系式为y=kx+b(k≠0),
由题意,得方程组,![]() ,
,
解得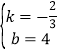 ,
,
所以,函数y与x的函数关系式为y=-![]() x+4;
x+4;
(2)由题意,P(x,y)是直线BC在第一象限的点,
∴y>0,且y=-![]() x+4,
x+4,
又,点A的坐标为(-2,0),点D的坐标为(1,0),
∴AD=3,
∴S△ADP=![]() ×3×〔-
×3×〔-![]() x+4 〕=-x+6,
x+4 〕=-x+6,
即S=-x+6;
(3)当S=3时,
-x+6=3,
解得x=3,
所以y=-![]() ×3+4=2,
×3+4=2,
此时,点P的坐标为(3,2).

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目