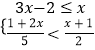��Ŀ����
����Ŀ���̳�����A��B������Ʒ�����ǵĽ��ۺ��ۼ������ʾ��
A��Ʒ | B��Ʒ | |
���ۣ�Ԫ/���� | 30 | 40 |
�ۼۣ�Ԫ/���� | 50 | 70 |
��1�������̳�����A��B������Ʒ��60����ǡ����ȥ2050Ԫ����A��B������Ʒ�����ټ���
��2�����̳��ڶ��ι���A��B������Ʒ����B��Ʒ������A��Ʒ������2����6�����ҹ����ܶ����2840Ԫ������������1900Ԫ������������̳������Ӧ�Ľ���������
��3����һ�����ڸ��̳�����A��B������Ʒ��������ǡ����140Ԫ��������A��B������Ʒ�����ټ���
���𰸡�
��1���⣺����̳�����A����Ʒx����B����Ʒy����������ã�
![]() ��
��
��� ![]() ��
��
�𣺸��̳�����A����Ʒ35����B����Ʒ25����
��2���⣺����̳�����A����Ʒa������B����Ʒ��2a��6��������������ã�
![]() ��
��
���26��a�� ![]() ��
��
��a����������
��a=26��27��28��
���Խ������������֣�
����һ������A����Ʒ26��������B����Ʒ46��
������������A����Ʒ27��������B����Ʒ48��
������������A����Ʒ28��������B����Ʒ50��
��3���⣺����̳�����A����Ʒb��������B����Ʒc������������ɵã�20b+30c=140��
��������
2b+3c=14
bֻ��ȡ1��4��
����A����Ʒ1����B����Ʒ4��������A����Ʒ4����B����Ʒ2����
����������1���ɡ�A��B������Ʒ��60������x+y=60���ɡ�ǡ����ȥ2050Ԫ���ɵ�30x+40y=2050���ⷽ���鼴�ɣ���2�����A����Ʒa�����ɡ�B��Ʒ������A��Ʒ������2����6�����ҹ����ܶ����2840Ԫ���ɵò���ʽ30a+40(2a6)��2860���ɡ�����������1900Ԫ���ɵò���ʽ20a+30(2a6)��1900���ⲻ��ʽ�飬�ҳ������⣬���������⣬���м��ַ�������3���ɡ�������ǡ����140�����ж�Ԫһ�η���20b+30c=140����������⼴��.
�����㾫����������Ҫ������һԪһ�β���ʽ���Ӧ�õ����֪ʶ�㣬��Ҫ����1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸲�����ȷ�����⣮

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�