��Ŀ����
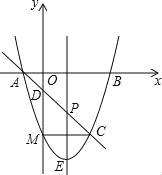
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����A��C������ֱ�Ϊ��-1��0������0��-3����ֱ��x=1Ϊ�����ߵĶԳ��ᣮ��DΪ�����ߵĶ��㣬ֱ��BC��Գ�������ڵ�E��
��1���������ߵĽ���ʽ��ֱ��д����D�����ꣻ
��2����PΪֱ��x=1�ҷ��������ϵ�һ�㣨��P�����B�غϣ�����A��B��C��P�ĵ������ɵ��ı������ΪS����S=![]() S��BCD�����P�����ꣻ
S��BCD�����P�����ꣻ
��3����Q���߶�BD�ϵĶ��㣬����DEQ�ӱ�EQ���۵õ���D��EQ���Ƿ���ڵ�Qʹ����D��EQ����BEQ���ص�����ͼ��Ϊֱ�������Σ������ڣ������BQ�ij����������ڣ���˵�����ɣ�
���𰸡�(1)y=x2-2x-3������D������Ϊ��1��-4������2��P������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ������3�����ڣ�
������3�����ڣ�![]() ��
��![]() 1��
1��![]() -
-![]() ��
��
��������
�����������1�����������ߵĶԳ��Եõ�B��3��0�������轻��ʽΪy=a��x+1����x-3������C��0��-3���������a���ɵõ������߽���ʽ��Ȼ��ѽ���ʽ��ɶ���ʽ���ɵõ�D�����ꣻ
��2����P��m��m2-2m-3������ȷ��ֱ��BC�Ľ���ʽy=x-3����ȷ��E��1��-2������ɸ��������������ʽ�����S��BDC=S��BDE+S��CDE=3��Ȼ��������ۣ�����P��x���Ϸ�ʱ����m��3����ͼ1������S=S��PAB+S��CAB=![]() S��BCD�õ�2m2-4m=
S��BCD�õ�2m2-4m=![]() ������P��x���·�ʱ����1��m��3����ͼ2������OP������S=S��AOC+S��COP+S��POB=
������P��x���·�ʱ����1��m��3����ͼ2������OP������S=S��AOC+S��COP+S��POB=![]() S��BCD�õ�-
S��BCD�õ�-![]() m2+
m2+![]() m+6=
m+6=![]() ���ٷֱ�����m��һԪ���η������m���Ӷ��õ�P�����ꣻ
���ٷֱ�����m��һԪ���η������m���Ӷ��õ�P�����ꣻ
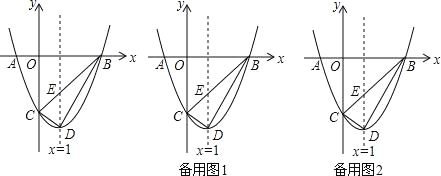
��3�����ڣ�ֱ��x=1��x����F�����������ľ��빫ʽ�����BD=2![]() ���������ۣ�����ͼ3��EQ��DB��Q��֤��Rt��DEQ��Rt��DBF���������Ʊȿɼ����DQ=
���������ۣ�����ͼ3��EQ��DB��Q��֤��Rt��DEQ��Rt��DBF���������Ʊȿɼ����DQ=![]() ����BQ=BD-DQ=
����BQ=BD-DQ=![]() ������ͼ4��ED����BD��H��֤��Rt��DEQ=H��Rt��DBF���������Ʊȼ����DH=
������ͼ4��ED����BD��H��֤��Rt��DEQ=H��Rt��DBF���������Ʊȼ����DH=![]() ��EH=
��EH=![]() ����Rt��QHD������QH=x��D��Q=DQ=DH-HQ=
����Rt��QHD������QH=x��D��Q=DQ=DH-HQ=![]() -x��D��H=D��E-EH=DE-EH=2-
-x��D��H=D��E-EH=DE-EH=2-![]() �������ù��ɶ����ɵ�x2+��2-
�������ù��ɶ����ɵ�x2+��2-![]() ��2=��
��2=��![]() -x��2�����x=1-
-x��2�����x=1-![]() ������BQ=BD-DH+HQ-
������BQ=BD-DH+HQ-![]() =
=![]() +1������ͼ5��D��Q��BC��G����EI��BD��I�����âٵý��ۿɵ�EI=
+1������ͼ5��D��Q��BC��G����EI��BD��I�����âٵý��ۿɵ�EI=![]() ��BI=
��BI=![]() ����BE=2
����BE=2![]() ����BG=BE-EG=2
����BG=BE-EG=2![]() -
-![]() �������۵����ʵ���EQD=��EQD�䣬����ݽ�ƽ�������ʵ�EG=EI=
�������۵����ʵ���EQD=��EQD�䣬����ݽ�ƽ�������ʵ�EG=EI=![]() ������֤����BQG�ס�BEI���������Ʊȿɵ�BQ=
������֤����BQG�ס�BEI���������Ʊȿɵ�BQ=![]() -
-![]() �����Ե�BQΪ
�����Ե�BQΪ![]() ��
��![]() +1��
+1��![]() -
-![]() ʱ������DEQ�ر�EQ���۵õ���D��EQ��ʹ����D��EQ����BEQ���ص�����ͼ��Ϊֱ�������Σ�
ʱ������DEQ�ر�EQ���۵õ���D��EQ��ʹ����D��EQ����BEQ���ص�����ͼ��Ϊֱ�������Σ�
�����������1������A���B����ֱ��x=1�Գƣ�
��B��3��0����
�������߽���ʽΪy=a��x+1����x-3����
��C��0��-3�������-3a=-3�����a=1��
�������߾�Ц��˵Ϊy=��x+1����x-3��=x2-2x-3��
��y=��x-1��2-4��
�������߶���D������Ϊ��1��-4����
��2����P��m��m2-2m-3������ֱ��BC�Ľ���ʽΪy=x-3��
��x=1ʱ��y=x-3=-3����E��1��-2����
��S��BDC=S��BDE+S��CDE=![]() ��3����-2+4��=3��
��3����-2+4��=3��
����P��x���Ϸ�ʱ����m��3����ͼ1��
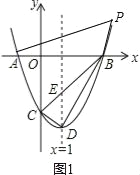
S=S��PAB+S��CAB=![]() 3��3+1��+
3��3+1��+![]() ��3+1����m2-2m-3��=2m2-4m��
��3+1����m2-2m-3��=2m2-4m��
��S=![]() S��BCD��
S��BCD��
��2m2-4m=![]() ��
��
������4m2-8m-15=0�����m1=![]() ��m2=
��m2=![]() ����ȥ����
����ȥ����
��P��������![]() ��
��![]() ����
����
����P��x���·�ʱ����1��m��3����ͼ2������OP��
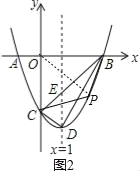
S=S��AOC+S��COP+S��POB=![]() 31+
31+![]() 3m+
3m+![]() 3��-m2+2m+3��=-
3��-m2+2m+3��=-![]() m2+
m2+![]() m+6��
m+6��
��S=![]() S��BCD��
S��BCD��
��-![]() m2+
m2+![]() m+6=
m+6=![]() ��
��
������m2-3m+1=0�����m1=![]() ��m2=
��m2=![]() ����ȥ��
����ȥ��
��P��������![]() ��
��![]() ����
����
����������P��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��3�����ڣ�ֱ��x=1��x����F��BD=![]() ��
��
����ͼ3��EQ��DB��Q����DEQ�ر�EQ���۵õ���D��EQ��

�ߡ�EDQ=��BDF��
��Rt��DEQ��Rt��DBF��
��![]() ����
����![]() �����DQ=
�����DQ=![]() ��
��
��BQ=BD-DQ=2![]() -
-![]() =
=![]() ��
��
����ͼ4��ED����BD��H��
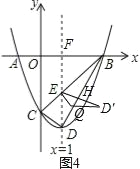
�ߡ�EDH=��BDF��
��Rt��DEQ=H��Rt��DBF��
��![]() ����
����![]() �����DH=
�����DH=![]() ��EH=
��EH=![]() ��
��
��Rt��QHD������QH=x��D��Q=DQ=DH-HQ=![]() -x��D��H=D��E-EH=DE-EH=2-
-x��D��H=D��E-EH=DE-EH=2-![]() ��
��
��x2+��2-![]() ��2=��
��2=��![]() -x��2�����x=1-
-x��2�����x=1-![]() ��
��
��BQ=BD-DQ=BD-��DH-HQ��=BD-DH+HQ=2![]() -
-![]() +1-
+1-![]() =
=![]() +1��
+1��
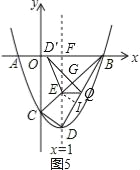
����ͼ5��D��Q��BC��G����EI��BD��I���ɢٵ�EI=![]() ��BI=
��BI=![]() ��
��
��BE=![]() ��
��
��BG=BE-EG=2![]() -
-![]() ��
��
�ߡ�DEQ�ر�EQ���۵õ���D��EQ��
���EQD=��EQD�䣬
��EG=EI=![]() ��
��
�ߡ�GBQ=��IBE��
���BQG�ס�BEI��
��![]() ����
����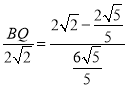
��BQ=![]() -
-![]() ��
��
������������BQΪ![]() ��
��![]() 1��
1��![]() -
-![]() ������DEQ�ر�EQ���۵õ���D��EQ��ʹ����D��EQ����BEQ���ص�����ͼ��Ϊֱ�������Σ�
������DEQ�ر�EQ���۵õ���D��EQ��ʹ����D��EQ����BEQ���ص�����ͼ��Ϊֱ�������Σ�