Question

【题目】阅读下面材料：

小明观察一个由1×1正方形点阵组成的点阵图，图中水平与竖直方向上任意两个相邻点间的距离都是1．他发现一个有趣的问题：对于图中出现的任意两条端点在点阵上且互相不垂直的线段，都可以在点阵中找到一点构造垂直，进而求出交点与垂足之间的数值．

请回答：

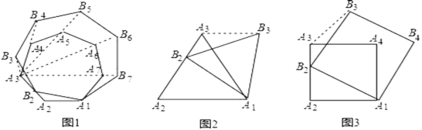
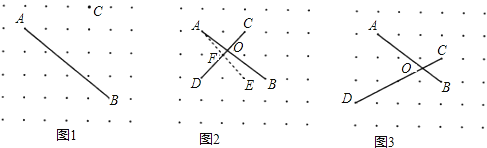
（1）如图1，A、B、C是点阵中的三个点，请在点阵中找到点D，作出线段CD，使得CD⊥AB；

（2）如图2，线段AB与CD交于点O，小明在点阵中找到了点E，连接AE．恰好满足AE⊥CD于E，再作出点阵中的其它线段，就可以构造相似三角形，经过推理和计算能够使问题得到解决．

请你帮小明计算：OC＝　 　OF＝　 　；

参考小明思考问题的方法，解决问题：

（3）如图3，线段AB与CD交于点O．在点阵中找到点E，连接AE，满足AE⊥CD于F．计算： OC＝　 　，OF＝　 　．

Answer 1

【答案】（1）详见解析；（2），；（3），．

【解析】

（1）利用数形结合的思想解决问题即可．

（2）利用相似三角形的性质解决问题即可．

（3）构造相似三角形解决问题即可．

（1）如图线段CD即为所求．

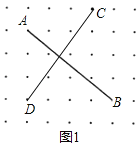
（2）连接AC，BD．

由题意AC＝2，DB＝3，CD＝＝2，

∵AC∥BD，

∴△ACO∽△BDO，

∴，

∴OC＝CD＝，

∵AC∥DE，

∴△ACF∽△EDF，

∴＝1，

∴DF＝CF＝，

∴OF＝CF﹣OC＝﹣＝．

故答案为，．

（3）如图3中，线段AE即为所求．

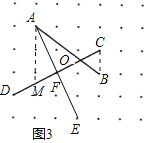
连接BC，作AM∥BC交CD于M．

由题意：BC＝1，AM＝2.5，CD＝2，DF＝CF＝，CM＝，

∵BC∥AM，

∴△BOC∽△AOM，

∴，

∴OC＝CM＝．

∴OF＝CF﹣OC＝＝．

故答案为，．