题目内容
15．已知13x3+mx2+11x+n能被13x2-6x+5整除，求m、n的值．分析 把多项式的除法进行竖式演算，根据题意得出商式，即可求出m．
解答 解：∵13x3+mx2+11x+n能被13x2-6x+5整除，
∴13x3+mx2+11x+n=（13x2-6x+5）（x-1）=13x3-19x2+11x-5，
∴m=-19，n=-5．
点评 本题考查了多项式的除法；可用竖式演算得出结果，即可解决问题．
练习册系列答案
相关题目
5．任意抛掷一枚硬币2次，两次都正面朝上的概率（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{4}$ |
图中∠AED分别为△ADE，△ABE中AD，AB边所对的角，在△AFD中，∠AFD是边AF，ED组成的角．
如图，抛物线y=ax2+bx+c与x轴的交点坐标是（-2，0），（3，0），则当y＞0时，x的取值范围是x＜-2或x＞3．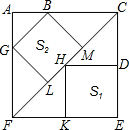
如图，边长为6的大正方形中有两个小正方形，两个小正方形的面积分别为S1、S2
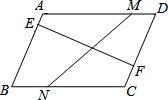如图，四边形ABCD为平行四边形，M，N两点分别从点D到点A、点B到点C运动，速度相同；E，F两点分别从点A到点B，点C到点D运动，速度相同．它们之间用橡皮筋连接．
10．在下列方程中，没有实数根的是（ ）
| A． | x2+2x-1=0 | B． | x2+2$\sqrt{2}$x+2=0 | C． | x2+$\sqrt{2}$x+1=0 | D． | -x2+2x+2=0 |