Question

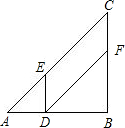在Rt△ABC中，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC．
（1）试写出四边形DFCE的面积S（cm²）与时间t（s）之间的函数关系式并写出自变量t的取值范围．
（2）试求出当t为何值时四边形DFCE的面积为20cm²？
（3）四边形DFCE的面积能为40cm²吗？如果能，求出D到A的距离；如果不能，请说明理由．

Answer 1

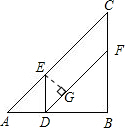解：（1）ts后，AD=2t，DB=12-2t
过E作EG⊥DF交DF于G点，
S_□CEDF=DF×EG=DB×DE×DB×DA
=DB×DA=（12-2t）×2t=-4t²+24t，（0＜t＜6）；

（2）S_□CEDF=DF×EG=-4t²+24t=20，即t²-6t+5=0，
解得t=1或5；当t为1或5时四边形DFCE的面积为20cm²

（3）S_□CEDF=DF×EG=-4t²+24t=-4（t²-6t）
所以当t=3时，四边形DFCE的面积最大，为S_□CEDF=36cm²
因此四边形DFCE的面积不可能为40．
分析：（1）根据四边形DFCE的面积公式即可求得S关t的二次函数；
（2）四边形DFCE的面积公式S_□CEDF=DF×EG=-4t²+24t=20，即可求得t为何值时四边形DFCE的面积为20cm²．
（3）根据二次函数的最值的求法求得四边形DFCE的最大面积为36，因此四边形DFCE的面积能为40cm²
点评：本题结合四边形的面积公式考查了二次函数的求法以及二次函数的最值问题，是各地中考的热点，学生在训练时应该加强．