题目内容
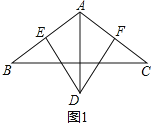
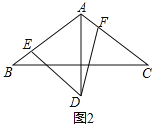
【题目】以下四个命题：①全等三角形的面积相等；②最小角等于50°的三角形是锐角三角形；③等腰△ABC中，D是底边BC上一点，E是一腰AC上的一点，若∠BAD=60°且AD=AE，则∠EDC=30°；④将多项式
因式分解，其结果为-y(2x+1)(x-3)．其中正确命题的序号为___________.
【答案】①②③④.
【解析】
根据全等三角形的性质，锐角三角形的性质，等腰三角形的性质以及因式分解对上述选项依次进行判定.
①根据全等三角形的性质得全等三角形的面积相等，正确；
②最小角等于50°的三角形，则最大角不超过180°-50°-50°=80°，所以为锐角三角形，则选项正确；
③∵∠AED=∠C+∠EDC=∠B+∠EDC，
∴∠ADC=∠ADE+∠EDC=∠AED+∠EDC=∠B+2∠EDC，
又∵∠ADC=∠B+∠BAD=∠B+60°，
∴∠B+2∠EDC=∠B+60°，
∴∠EDC=30°，
故③正确；
④
= -y(2x+1)(x-3),故选项正确.
答案为①②③④.
练习册系列答案
相关题目
【题目】深圳市政府计划投资1.4万亿元实施东进战略．为了解深圳市民对东进战略的关注情况．某校数学兴趣小组随机采访部分深圳市民，对采访情况制作了统计图表的一部分如下：
关注情况 | 频数 | 频率 |
A．高度关注 | M | 0.1 |
B．一般关注 | 100 | 0.5 |
C．不关注 | 30 | N |
D．不知道 | 50 | 0.25 |
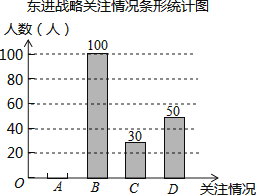
（1）根据上述统计图可得此次采访的人数为人，m= ， n=
（2）根据以上信息补全条形统计图；
（3）根据上述采访结果，请估计在15000名深圳市民中，高度关注东进战略的深圳市民约有人．
