题目内容
使得函数值为零的自变量的值称为函数的零点.例如,对于函数 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 的零点.请根据零点的定义解决下列问题:已知函数
的零点.请根据零点的定义解决下列问题:已知函数 (m为常数).
(m为常数).
1.当m=0时,求该函数的零点
2.证明:无论m取何值,该函数总有两个零点;
3.设函数的两个零点分别为 和
和 ,且
,且 ,此时函数图象与
,此时函数图象与 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式.
上,当MA+MB最小时,求直线AM的函数解析式.
1.函数的零点为 和-
和- .。
.。
2.见解析。
3.
【解析】解:(1)当 时,
时, ,
-------1分
,
-------1分
令 ,即
,即 ,解得
,解得 ,
,
∴当 时,该函数的零点为
时,该函数的零点为 和-
和- . ………………………2分
. ………………………2分
(2)令 ,即
,即 ,
,
△=(-2m)2-4[-2(m+3)] =4m2+8m+24………………………1分
△=4(m+1)2+20
∵无论m为何值,4(m+1)2≥0,4(m+1)2+20>0, 即△>0,………………2分
∴无论m为何值,方程 总有两个不相等的实数根,
总有两个不相等的实数根,
即该函数总有两个零点. ………………………3分
(3)依题意有, ,
, , …………………1分
, …………………1分
由 得
得 =-
=- ,即
,即 =-
=- ,……………2分
,……………2分
解得m=1. …………………3分
因此函数解析式为y=x2-2x-8,
令y=0,解得x1=-2,x2=4,
∴A(-2,0),B(4,0), …………………4分
作点B关于直线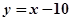 的对称点B´,连结AB´,
的对称点B´,连结AB´,
则AB´与直线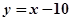 的交点就是满足条件的M点. …………………5分
的交点就是满足条件的M点. …………………5分
易求得直线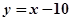 与x轴、y轴的交点分别为C(10,0),D(0,-10),………6分
与x轴、y轴的交点分别为C(10,0),D(0,-10),………6分
连结CB´,则∠BCD=45°,∴BC=CB´=6,∠B´CD=∠BCD=45°,
∴∠BCB´=90°. 即B´(10,-6). ………7分
设直线AB´的解析式为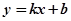 ,则
,则
 ,解得
,解得 ,
, .
.
∴直线AB´的解析式为 ,
,
即AM的解析式为 .
.

 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 (m为常数).
(m为常数). 和
和 ,且
,且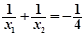 ,此时函数图象与
,此时函数图象与 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线 上,当MA+MB最小时,求直线AM的函数解析式.
上,当MA+MB最小时,求直线AM的函数解析式. ,令y=0,可得x=1,我们就说1是函数
,令y=0,可得x=1,我们就说1是函数 (
( m为常数)。
m为常数)。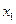 和
和 ,且
,且 ,此时函数图象与x轴的交点分
,此时函数图象与x轴的交点分 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。 ,令
,令 ,可得
,可得 ,我们就说
,我们就说 是函数
是函数 (k为常数).当k=2时,求该函数的零点;
(k为常数).当k=2时,求该函数的零点;