Question

甲题：已知关于x的一元二次方程x²=2（1-m）x-m²的两实数根为x₁，x₂．
（1）求m的取值范围；
（2）设y=x₁+x₂，当y取得最小值时，求相应m的值，并求出最小值．
乙题：如图，梯形ABCD中，AD∥BC，点E是边AD的中点，连接BE交AC于点F，BE的延长线交CD的延长线于点G．
（1）求证：；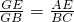
（2）若GE=2，BF=3，求线段EF的长．

Answer 1

甲题：解：（1）∵一元二次方程x²=2（1-m）x-m²的两实数根，
∴x²-2（1-m）x+m²=0，
∵△=b²-4ac=[-2（1-m）]²-4m²=4-8m≥0，
∴m≤；

（2）∵一元二次方程x²=2（1-m）x-m²，即x²-2（1-m）x+m²=0，
∴x₁+x₂=2-2m，
∴y=x₁+x₂=-2m+2，
∵-2＜0，
∴y随m的增大而减小，
∵m≤，
∴当m=时，y有最小值y=-2m+2=1；

乙题：证明：（1）∵AD∥BC，
∴△GED∽△GBC，
∴=，
∵点E是边AD的中点，
∴AE=DE，
∴=；

（2）∵AD∥BC，
∴△AEF∽△CBF，
∴=，
由（1）得：=，
∴=，
设EF=x，∵GE=2，BF=3，
∴=，
整理得，x²+5x-6=0，
解得x₁=1，x₂=-6（不合题意，舍去），
∴EF=1．
故答案为：1．
分析：甲题：（1）根据一元二次方程有两个实数根，判别式△≥0列式求解即可；
（2）利用根与系数的关系表示出y与m的函数关系，再根据一次函数的增减性解答；
乙题：（1）根据AD∥BC可得△GED和△GBC相似，再根据相似三角形对应边成比例列出比例式=，再根据中点定义可得AE=DE，等量代换即可得证；
（2）根据AD∥BC可得△AEF和△CBF相似，再根据相似三角形对应边成比例可得=，然后设EF=x，与（1）的结论联立得到关于x的方程求解即可．
点评：甲题考查了一元二次方程根的判别式与根与系数的关系，比较简单，①△＞0，一元二次方程有两个不相等的实数根，②△=0，一元二次方程有两个相等的实数根，③△＜0，一元二次方程没有实数根；
乙题考查了相似三角形的判定与性质，由平行线判定相似三角形是最常用的方法，（2）利用中间量得到比例式然后整理出一元二次方程是解题的关键．